
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры термодинамических потенциалов
|
|
|
|
1) Выберем в качестве независимых параметров объём V и энтропию S. Тогда из основного уравнения термодинамики получаем:  , откуда находим
, откуда находим  ,
,  . Следовательно, внутренняя энергия
. Следовательно, внутренняя энергия  - потенциал.
- потенциал.
Смысл внутренней энергии как потенциала: при V=const получаем  , т.е. изменение внутренней энергии равно количеству теплоты, подведенной к системе при изохорном процессе.
, т.е. изменение внутренней энергии равно количеству теплоты, подведенной к системе при изохорном процессе.
Если процесс необратимый, то  или
или  .
.
2) Выберем в качестве независимых параметров давление p и энтропию S.
С учетом равенства  и основного уравнения термодинамики
и основного уравнения термодинамики  , получаем, прибавляя в правую и левую части основного уравнения слагаемое Vdp,:
, получаем, прибавляя в правую и левую части основного уравнения слагаемое Vdp,: 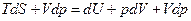 , откуда следует:
, откуда следует:  .
.
Введем обозначение  . Тогда
. Тогда  и
и  ,
,  . Значит, функция
. Значит, функция  является термодинамическим потенциалом и носит название: энтальпия.
является термодинамическим потенциалом и носит название: энтальпия.
Смысл энтальпии как термодинамического потенциала: при p =const получаем, что 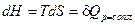 , т.е. изменение энтальпии равно подведенному количеству теплоты при изобарном процессе.
, т.е. изменение энтальпии равно подведенному количеству теплоты при изобарном процессе.
Если процесс необратимый, то  или
или  ,
,  .
.
3) Выберем в качестве независимых параметров объём V и температуру T.
Перепишем основное уравнение термодинамики  в виде
в виде  и с учётом равенства
и с учётом равенства  получаем:
получаем:  или
или  .
.
Вводим обозначение  , тогда
, тогда  ,
,  ,
,  . Таким образом,
. Таким образом,  - термодинамический потенциал, который называется свободной энергией или термодинамическим потенциалом Гельмгольца.
- термодинамический потенциал, который называется свободной энергией или термодинамическим потенциалом Гельмгольца.
Смысл свободной энергии как термодинамического потенциала: при T=const получаем  , т.е. уменьшение свободной энергии равно работе совершенной системой в изотермическом процессе.
, т.е. уменьшение свободной энергии равно работе совершенной системой в изотермическом процессе.
Если процесс необратимый, то  или
или  , т.е.
, т.е.
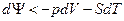 .
.
При необратимых изотермическом и изохорном процессах  - свободная энергия уменьшается до тех пор, пока система не придет в термодинамическое равновесие – в этом случае свободная энергия принимает минимальное значение.
- свободная энергия уменьшается до тех пор, пока система не придет в термодинамическое равновесие – в этом случае свободная энергия принимает минимальное значение.
4) Выберем в качестве независимых параметров давление p и температуру T.
Рассмотрим функцию  ,
,
 ,
,
 .
.
Так как  и
и 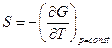 , то
, то 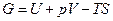 - потенциал, который носит название энергия Гиббса (термодинамический потенциал Гиббса).
- потенциал, который носит название энергия Гиббса (термодинамический потенциал Гиббса).
Если процесс необратимый, то, 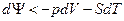 и
и  , поэтому
, поэтому 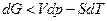 .
.
Для изобарного и изотермического необратимых процессов энергия Гиббса убывает и при достижении равновесия принимает минимальное значение. Между термодинамическими потенциалами можно установить соотношения.
Из соотношений  ,
,  получаем уравнение Гиббса-Гельмгольца:
получаем уравнение Гиббса-Гельмгольца:  .
.
Зависимость энтальпии от потенциала Гиббса:  .
.
Внутренняя энергия система с переменным числом частиц изменяется не только за счет сообщения теплоты и совершения работы системой, но и за счет изменения числа частиц в системе, поэтому
 ,
,
где k – сорт частиц, dNk – изменение числа частиц k -го сорта. При этом изменение массы системы 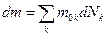 , где m 0 k – масса частиц k -го сорта.
, где m 0 k – масса частиц k -го сорта.
Для равновесных процессов 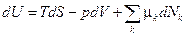 .
.
Величина  называется химическим потенциалом частиц k -го сорта.
называется химическим потенциалом частиц k -го сорта.
По физическому смыслу – это энергия, приходящаяся на одну частицу.
Найдем связь химического потенциала с другими термодинамическими потенциалами.
1) Энтальпия  ,
,
 .
.
Откуда  .
.
2) Свободная энергия (Гельмгольца)  ,
,
 .
.
Откуда  .
.
3) Энергия Гиббса 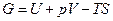 ,
,
 .
.
Откуда  .
.
Итак 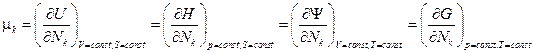 .
.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 800; Нарушение авторских прав?; Мы поможем в написании вашей работы!