Целевая функция и ее весовая характеристика

В альтернативном подходе (целевое программирование) целевая функция, минимизирующая максимальные потери, заменяется суммой абсолютных потерь

.

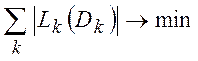Еще один подход к поиску компромиссного решения задачи многокритериального планирования основан на предположении, аддитивности что функция полезности всей системы является взвешенной суммой частных критериев полезности (аддитивность свойства полезности). Обозначив вес цели 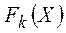через 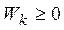, запишем целевую функцию (полезность всей системы) в виде 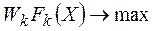, где сумма относительных весов равна 1 и единицы измерения каждой цели 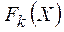одинаковы.

Рис.1. Множество осуществимых решений для двухкритериальных задач:

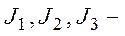линии равного предпочтения или критерии безразличия;

abcde – граница множества достижимости или кривая взаимозаменяемости целей

Изменяя относительные веса , можно получить выпуклую часть границы множества допустимых планов.

Если части abc и de кривой выпуклы, а часть границы множества достижимости cd не выпукла или, как ab, не содержит эффективных по Парето точек, то максимизация различных взвешенных сумм частей цели не дает всех точек границ. В этом случае границу можно определить, фиксируя величину некоторых частных целей и максимизируя сумму других.

Если критерии 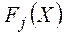не выражаются в одних единицах, то определяется масштабная функция так, чтобы диапазон изменения каждого критерия 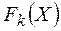ограничивался одними и теми же числами, например, от 0 до 1.

Максимум 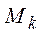получается из , если 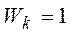, а все другие веса равны 0. Если 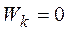и выбирается минимум всех целей, взятых с разными весами, то определяется минимум .

Целевая функция принимает вид

,

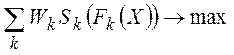где относительные веса 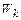принимают значения на отрезке [0,1] и их сумма равна 1.

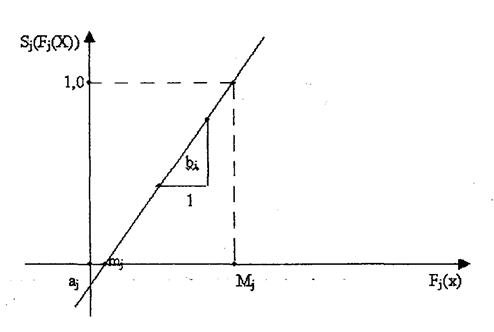
Рис.2. Масштабирование значений целевой функции:

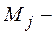максимум целевой функции; 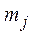- минимум целевой функции

Каждая масштабная функция отображает множество значений целевой функции на интервал от 0 до 1 (рис.2).

Масштабную функцию можно определить как 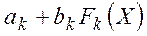, где

.

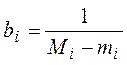В рамках линейных масштабных функций целевая функция запишется в ви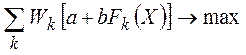де

, где - константа, которую при оценке компромисса между целями 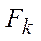можно не учитывать.

Комбинирование масштабирующего множителя с относительными весами производится так, чтобы общая сумма была равна 1.

Неотрицательные веса 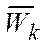, сумма которых равна 1, включает относительные веса W_k и масштабные коэффициенты

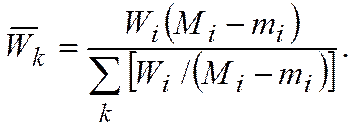
Целевая функция принимает вид .

Изменяя относительные веса 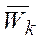от 0 до 1 при условии нормировки 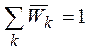, можно определить компромиссы между целями .

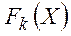На стадии формирования плана появляются альтернативы . Каждый план - вектор выбранных переменных, удовлетворяющий определенным уровням целей (j =1,2,..., n). План должен удовлетворять условиям технологической осуществимости (j =1,2,..., m) и в идеале быть оптимальным по Парето. Это означает, что возрастание одной целевой функции возможно только при убывании других целевых функций.

17. Понятие о кривой безразличия целевых функций системы.

При многокритериальном планировании проводится выбор решения в виде вектора 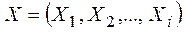, координаты которого представляют распределение дефицитных ресурсов (т.е. входные данные экономической системы), характеристики плана (т.е. выходные данные экономической системы) и плановые стратегии (т.е. перечень заранее намеченных управляющих воздействий). В дальнейшем при рассмотрении отдельных объектов планирования векторы Х будут именоваться технико-эксплуатационными элементами объекта (ТЭЭ). Определенные технические связи между переменными (i =1, 2,..., m) налагают ограничения на альтернативные планы или задают пределы технической достижимости. Для отдельных объектов проектирования эти ограничения принимают характер параметров технических решений (ПТР). Если предпочтение лица, принимающего решения, выражено критерием F (X), величина которого для вектора Х выражает полезность решения, то заданная модель однокритериальна. Для двух переменных 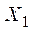и 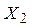и критерия F (X), который должен принять максимум, может быть построен график стратегии (рис.3.1).

При многокритериальном планировании производится выбор плана 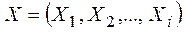, удовлетворяющего ограничениям 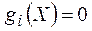i =1,2,..., m, и наилучшим образом удовлетворяющего критериям 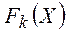, k =l,2,..., n.

В результате сравнения двух планов и 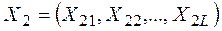первый может оказаться достигающим более высокого уровня первой цели. За исключением крайних случаев, когда для всех целей 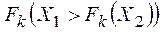(т.е. когда 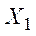для всех критериев лучше ) или 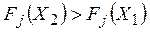(т.е. когда 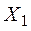для всех критериев хуже 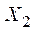), выбор плана ведет к уменьшению одной целевой функции за счет увеличения других.

В предположении, что ЛПР устанавливает минимальные уровни целей для технически реализуемого плана, запишем 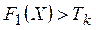, и 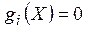, для всех и .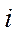

Если уровни целе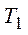й и 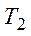известны, а план Х при 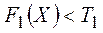отвергается, то никакой уровень не может компенсировать потерю 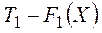. Ниже определенного минимального уровня никакой компромисс между целями невозможен.

Каждый допустимый ограничениями 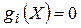(i =l,2,..., m) план X определяет пару величин 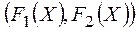и может быть представлен соответствующей точкой на плоскости (рис.). Пусть каждое вектор-решение на участке abcde задает максимум при заданном 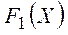. Легко видеть, что на границе bcde нельзя добиться увеличения одной целевой функции, не уменьшив другую.

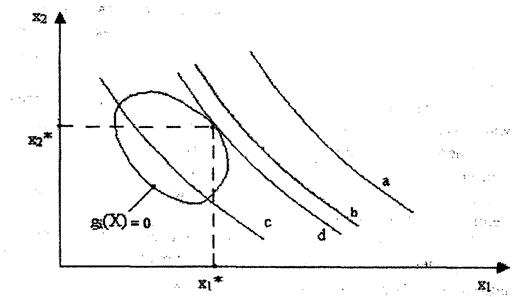
Рис. Стратегии для двух переменных:

а, b, с - линии уровня цели 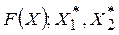- оптимальное решение на множестве,

заданном ограничениями

Планы, лежащие на этой части кривой, называются эффективными по Парето (эффективными в том смысле, что среди них находится оптимальный компромиссный план). Решения на части аb не эффективны в том смысле, что они могут доминироваться решениями (в точке b), дающими лучшие значения обеих целевых функций. Поэтому не эффективные по Парето участки кривой abcde должны быть исключены из рассмотрения.

Каждая точка на кривой взаимозаменяемости соответствует определенному компромиссу или маргинальной взаимозаменяемости между целями, на что указывает наклон кривой. Планы b, c, и d соответствуют трем различным маргинальным взаимозаменяемостям целей и 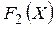. Кривые безразличия определяются как совокупности точек с одинаковым предпочтением.

18. Алгоритм итеративной процедуры пошагового метода (Step method).

Итеративная процедура СТЕМ (Step method - пошаговый метод). Здесь предполагается, что относительная важность целей заранее не определена. Пусть есть n альтернатив, каждая из которых максимизирует одну из n целей. На первой итерации минимизируется максимальная взвешенная разность между целью 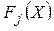и соответствующим ей максимальным значением или 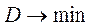при условиях 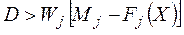, 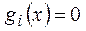при вcex j и i.

Ограничение для D означает, что каждая взвешенная разность не меньше разности между максимальным и действительным значениями каждой цели.

Вес W_j определяется как отношение параметра чувствительности Y_j к масштабному параметру 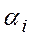в виде .

Величина 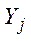, равна

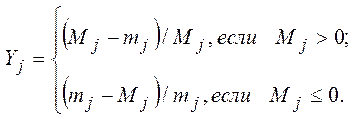
и является относительным диапазоном значения цели .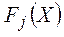

Знаменатель используется для масштабирования относительных весов так, чтобы их сумма была равна 1. Первоначально эта константа равна

,

где, если M_j <0 для хотя бы одного j, то К =1-min M_j, иначе К =0.

На следующих итерациях относительные веса тех целей, значения которых удовлетворительны, принимаются равными нулю и, таким образом, получается суммирование только по тем целям, значения которых неудовлетворительны.

При нормировании значений всех целей так, чтобы суммы относительных весов были равны единице, оказывается, что можно сравнивать решения, полученные из постановок с различными весами. Решением на первой итерации будет план Х_о, который дается вектором значений целей Z_o=[F₁(X_о),..., F_n(X_o) ].

Сравнивая эти результаты с идеальным вектором целей Z=[M₁,М₂,...,М_n], определяют значение наиболее удовлетворительной цели и уменьшают ее значение. На следующей итерации улучшаются значения неудовлетворительных компонент. Величина удовлетворительной функции 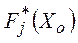уменьшается на допустимую величину .

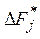Перед следующей итерацией относительные веса удовлетворительных целей берутся равными нулю и допустимые области изменяются наложением дополнительных ограничений:

.

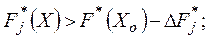
Члены d_j увеличиваются так, чтобы обеспечить равенство единице суммы относительных весов неудовлетворительных целей.

Итерации продолжаются до тех пор, пока компоненты целевого вектора Z либо станут удовлетворительными, либо будут неудовлетворительными.

В первом случае вектор-решение Х дает наилучший компромисс, а во втором случае решения не существует. Число итераций для n -критериальной задачи не превышает n. Когда наилучшее компромиссное решение получено, можно вычислить относительные веса из совместного решения уравнений .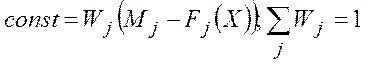

Дата добавления: 2014-01-06