
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Минимизация ФАЛ и ограничения при ее рассмотрении
|
|
|
|
Покажем на примере, что СДНФ не является экономной формой записи:
f(Х1, Х2)= Х1Х2 Х1Х2
Х1Х2 Х1Х2 =Х1
Х1Х2 =Х1 Х1 Х2
Х1 Х2
на основании полного склеивания по Х2 мы видим, что запись стала короче, т.к. содержит меньшее число связок и букв. Физически это означает, что устройство, которое реализует эквивалентную, но более простую функцию, будет иметь в своем составе меньшее количество оборудования, а следовательно, будет работать надежнее.
Итак, задача синтеза устройства должна быть дополнена задачей уменьшения оборудования в нем. С математической точки зрения это задача построения минимальной ФАЛ.
Под минимальной ФАЛ понимается такая форма, в которой содержится меньшее количество букв и членов, чем в ее исходной форме.
Речь идет именно о буквах, а не о переменных, так в функции:
f(Х1, Х2)= Х1Х2 Х1Х2
Х1Х2 Х1Х2 имеется 6 букв и только 2 переменных.
Х1Х2 имеется 6 букв и только 2 переменных.
Видно, что если какое-либо элементарное произведение входит в функцию, то при добавлении к нему новых сомножителей, полученное произведение так же будет входить в функцию.
Пример: если Х1Х2 входит в функцию от любого числа аргументов (>2), то в нее войдет, например, произведение Х1Х2Х3.
Это можно показать так:
f(Х1, Х2)= Х1Х2
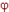 (Х1Х2)= Х1Х2 (Х3
(Х1Х2)= Х1Х2 (Х3 Х3)
Х3)
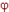 (Х1Х2)= Х1 Х2 Х3
(Х1Х2)= Х1 Х2 Х3  Х1 Х2 Х3
Х1 Х2 Х3 
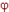 (Х1Х2)=Х1 Х2 Х3
(Х1Х2)=Х1 Х2 Х3 
 (Х1 Х2 Х3)
(Х1 Х2 Х3)
Дадим ряд определений:
- Произведение одной или нескольких неповторяющихся переменных, взятых с отрицанием или без него, называют элементарным.
Например, Х1 Х2 Х3 – элементарное произведение, т.к. в него входят различные буквы Х1 Х2 Х3.
- Дизъюнкция элементарных произведений – ДНФ.
- ДНФ является минимальной, если в ней минимальное число букв и членов.
- Конституентой единицы функции называют функцию, принимающую значение единицы только на одном наборе аргументов.
Обычно конституенты единицы выражают через произведение всех переменных, от которых зависит функция. СДНФ – дизъюнкция конституент единицы.
- Ранг произведения – число букв, входящих в него.
- Собственной частью называется произведение, полученное путем отбрасывания одной или нескольких переменных.
Например, Х1 Х2 Х3 Х4, где Х1, Х1 Х2, Х1 Х2 Х3 – некоторые собственные части.
- Если функция
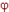 равна нулю на наборах аргументов, на которых обращается в нуль функция F, то говорят, что
равна нулю на наборах аргументов, на которых обращается в нуль функция F, то говорят, что 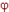 является импликантой функции F (т.е. нулей у импликанты не меньше, чем у функции).
является импликантой функции F (т.е. нулей у импликанты не меньше, чем у функции). - Простой импликантой называется произведение, которое само входит в выражение функции, но никакая его собственная часть в выражение функции не входит.
Например, Х1  Х1 Х2 Х3
Х1 Х2 Х3  Х1Х3=f: здесь Х1- простая импликанта, а Х1 Х2 Х3 и Х1 Х3 - не простые.
Х1Х3=f: здесь Х1- простая импликанта, а Х1 Х2 Х3 и Х1 Х3 - не простые.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 368; Нарушение авторских прав?; Мы поможем в написании вашей работы!