Потенциал электростатического поля

Работа электрического поля.

На любой электрический заряд, оказавшийся в электрическом поле, будет оказываться со стороны поля силовое действие (см. формулу (1-8)):

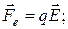(2-8)

Под действием этой силы свободный электрический заряд может перемещаться в поле. При перемещении заряда из точки 1 в точку 2 электрическое поле совершает механическую работу:

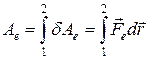. (2-9)

Покажем на примере взаимодействия двух точечных зарядов, что электрические силы – консервативные (потенциальные) силы, для них :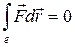

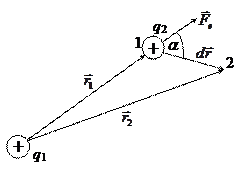
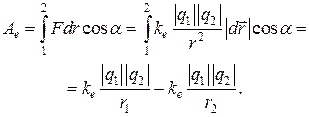
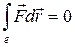
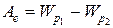
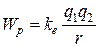- (2-10)

потенциальная энергия взаимодействия двух точечных электрических зарядов.

Циркуляцией вектора вдоль произвольного замкнутого контура ℓ называют интеграл:

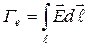. (2-11)

Теорема о циркуляции напряженности электростатического поля вдоль произвольного замкнутого контура ℓ утверждает, что электростатическое поле является потенциальным (безвихревым) и его силовые линии не замкнутые:

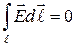. (2-12)

Работа электростатических сил по замкнутому контуру согласно теореме (2-12) и формуле (2-9) равна нулю. Это значит, что электростатические силы потенциальные (консервативные).

Второй основной характеристикой электрического поля является потенциал – энергетическая характеристика поля.

Потенциал электрического поля j в данной точке – физическая величина, равная отношению потенциальной энергии W_р, которой обладает пробный заряд q, помещенный в данную точку поля, к величине этого заряда:

j = 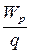. (2-13)

В Си потенциал j измеряется в вольтах (В).

Потенциал электрического поля, созданного точечным зарядом q на расстоянии r от него, вычисляется по формуле:

j = 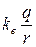. (2-14)

Потенциал – алгебраическая величина, которая может быть положительной и отрицательной в зависимости от знака заряда, создающего поле (j > 0 для q > 0; j < 0 для q < 0).

Разность потенциалов для двух точек электрического поля – скалярная физическая величина, равная отношению работы А_е, совершаемой электрическим полем по перемещению пробного электрического заряда q между этими точками, к величине этого заряда:

j ₁ - j ₂ = 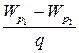= 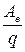(2-15)

(при действии на заряд только электрических сил разность потенциалов часто называют напряжением j ₁ - j ₂ = U).

В СИ разность потенциалов (напряжение) измеряется в вольтах (В).

Если электрическое поле создается несколькими зарядами, то в соответствии с принципом суперпозиции электрических полей можно записать:

j = j ₁ + j ₂ + … + j_n,

D j = (j ₂ - j ₁)₁ + (j ₂ - j ₁)₂ + … + (j ₂ - j ₁) _n. (2-16)

Потенциал (разность потенциалов) электростатического поля, созданного нескольким зарядами, равен (равна) алгебраической сумме потенциалов (разности потенциалов) полей отдельных зарядов.

Между двумя основными характеристиками электрического поля существует связь:

,

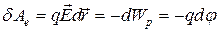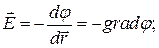(2-17)

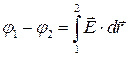. (2-18)

Например, для электрического поля точечного заряда:

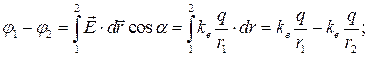. (2-18а)

для электрического поля бесконечно длинной заряженной нити:

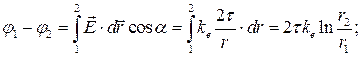. (2-18б)

для электрического поля бесконечно большой заряженной плоскости:

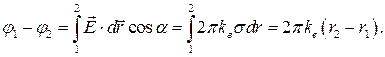. (2-18в)

Электрическое поле можно графически изобразить с помощью эквипотенциальных поверхностей.

Эквипотенциальные поверхности – это геометрическое место точек с одинаковым потенциалом (j = const). Силовые линии проходят перпендикулярно эквипотенциальным поверхностям в сторону уменьшения потенциала.

а б

В соответствии с (2-8), (2-9) и (2-17) в случае однородного электрического поля можно записать:

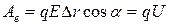, (2-19)

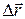где a - угол между вектором и перемещением заряда q между двумя точками поля с разностью потенциалов .

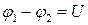Возможность влиять на движение заряженных частиц с помощью электрического поля широко используется в электронно-лучевых трубках, линейных ускорителях заряженных частиц и т. п.

Дата добавления: 2014-01-06