Информация о вкладах в банке для расчета средних значений

Вид вклада	Октябрь	Ноябрь
Число вкладов, тыс., f	Средний размер вклада, руб., x	Сумма вкладов, млн руб., w	Средний размер вклада, руб., x
До востребования Срочный			4,07 3,87

В октябре известен средний размер вкладов каждого вида х и количество вкладов f. Следовательно, для расчета среднего раз­мера вклада по двум видам применяем формулу средней ариф­метической взвешенной, руб.:

.

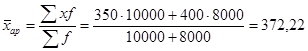В ноябре известен средний размер вкладов каждого вида, а количество вкладов — не известно, но зато имеются данные об общих суммах этих вкладов.

Путем деления сумм вкладов w каждого вида на их средний размер вклада х можно определить веса — число вкладов f по их видам, а затем определить средний размер вклада по двум видам по формуле средней арифметической взвешенной. Однако, если в расчете использовать среднюю гармоническую взвешенную, то отпадает необходимость предварительных расчетов весов - раз­меров вкладов по каждому виду, поскольку эта операция зало­жена в саму формулу.

Итак, средний размер вклада в ноябре по двум их видам на­ходим по формуле средней гармонической взвешенной, руб.:

.

.

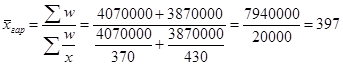5.2.4. Средняя геометрическая

Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.

Средняя геометрическая исчисляется извлечением корня степени я из произведений отдельных значений — вариантов признака х.

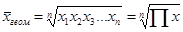(5.11, а)

где п - число вариантов; П - знак произведения.

Наиболее широкое применение средняя геометрическая по­лучила для определения средних темпов изменения в рядах ди­намики, а также в рядах распределения.

Использование средней геометрической показано в гл. 7.

5.2.5. Средняя квадратическая и средняя кубическая

В ряде случаев в экономической практике возникает по­требность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда при­меняется средняя квадратическая (например, для вычисления средней величины стороны п квадратных участков, средних диаметров труб, стволов и т.п.) и средняя кубическая (напри­мер, при определении средней длины стороны п кубов). Формулы для расчета средней квадратической:

Ø Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных зна­чений признака на их число:

; (5.12)

Ø средняя квадратическая взвешенная

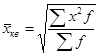, (5.13)

где - веса.

Формулы для расчета средней кубической ана­логичны:

Ø средняя кубическая простая

;

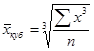(5.14)

Ø средняя кубическая взвешенная

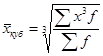. (5.15)

Средние квадратическая и кубическая имеют ограниченное применение в практике статистики. Широко пользуется стати­стика средней квадратической, но не из самих вариантов х, и из их отклонений от средней (х-) при расчете показателей ва­риации (см. 5.3).

Средняя может быть вычислена не для всех, а для какой-либо части единиц совокупности. Примером такой средней мо­жет быть средняя прогрессивная как одна из частных средних, вычисляемая не для всех, а только для "лучших" (например, для показателей выше или ниже средних индивидуальных).

5.2.6 Структурные средние

Особым видом средних величин являются структурные сред­ние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Ø Мода М_о — значение случайной величины, встречающее­ся с наибольшей вероятностью в дискретном вариационном ря­ду — вариант, имеющий наибольшую частоту.

Например, в табл.5.1 наибольшей частотой является число 5. Этой частоте соответствует модальное значение признака, т.е. выработка деталей за смену. Мода свидетельствует, что в дан­ном примере чаще всего встречаются рабочие, изготавливающие за смену 20 деталей.

В интервальных рядах распределения с равными интервала­ми мода вычисляется по формуле:

, (5.16)

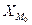- нижняя граница модального интервала; 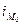- модальный интервал; ^— частоты в модальном, пре­дыдущем и следующем за модальным интервалах (соответственно). Модальный интервал определяется по наибольшей частоте.

По данным табл.5.4 рассчитаем моду, млн. руб.:

Итак, модальным значением стоимости ОПФ предприятий региона является стоимость, равная 18,8 млн руб.

Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т.п.

Ø Медиана М_е — это вариант, который находится в середи­не вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части — со значениями признака меньше медиа­ны и со значениями признака больше медианы. Чтобы найти медиану, необходимо отыскать значение признака, которое на­ходится в середине упорядоченного ряда. В ранжированных ря­дах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы.

Пусть ряд состоит из показателей заработной платы 9 рабо­чих, руб. в месяц (в 1996 г.):

630, 650, 680, 690, 700, 710, 720, 730, 750.

Номер медианы для нечетного объема вычисляется по формуле:

,

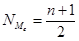где n— число членов ряда.

В нашем примере номер медианы равен 5, медиана равна 700 руб. (т.е. одна половина рабочих получила зарплату менее 700 руб., а другая — более 700 руб. в месяц).

В случае четного объема ряда медиана равна средней из двух вариантов, находящихся в середине ряда.

В интервальных рядах распределения медианное значение (по­скольку оно делит всю совокупность на две равные по численно­сти части) оказывается в каком-то из интервалов признака х. Этот интервал характерен тем, что его кумулятивная частота (накоп­ленная сумма частот) равна или превышает полусумму всех час­тот ряда. Значение медианы вычисляется линейной интерполяцией по формуле:

(5.17)

где 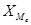- нижняя граница медианного интервала; 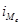- медианный интервал; - половина от общего числа наблюдений; сумма наблюдений, накопленная до начала медианного интервала;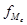 — число наблюдений в медианном интервале.

Формула (5.17) получена исходя из допущения о равномер­ности нарастания накоплений частоты внутри интервала и пригодна для любого интервального ряда.

Рассчитаем медиану по данным табл. 5.4. Прежде всего най­дем медианный интервал Таким интервалом, очевидно, будет интервал стоимости ОПФ предприятий (18—20 млн. руб.), по­скольку его кумулятивная частота равна 18 (2+6+10), что пре­вышает половину суммы всех частот (25: 2 = 12,5). Нижняя граница интервала 18 млн. руб., его частота 10; частота, накоп­ленная до него, равна 8.

Подставив данные в формулу (5.17), найдем значение меди­ан, млн. руб.:

Полученный результат говорит о том, что из 25 предприятий региона 12 предприятий имеют стоимость ОПФ менее 18 млн руб., а 12 предприятий — более.

Медиана находит практическое применение в маркетинговой деятельности вследствие особого свойства — сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая:

Мода и медиана в отличие от степенных средних являются конкретными характеристиками, их значение имеет какой-либо конкретный вариант в вариационном ряду.

Мода и медиана, как правило, отличаются от значения сред­ней, совпадая с ней только в случае симметричного распределе­ния частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить ассиметрию ряда распределения.

Мода и медиана, как правило, являются дополнительными к средней характеристиками совокупности и используются в мате­матической статистике для анализа формы рядов распределения.

Аналогично медиане вычисляются значения признака, деля­щие совокупность на четыре равные (по числу единиц) части — квартели, на пять равных частей — квинтели, на десять частей — децели, на сто частей — перцентели.

Использование в анализе вариационных рядов распределе­ния рассмотренных выше характеристик позволяет более глубо­ко и детально охарактеризовать изучаемую совокупность.

5.3.Показатели вариации

Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.

Например, работники фирмы различаются по доходам, за­тратам времени на работу, росту, весу, любимому занятию в свободное время и т.д.

Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному соче­таются в каждом отдельном случае. Таким образом, величина каждого варианта объективна.

Исследование вариации в статистике имеет большое значение, помогает познать сущность изучаемого явления. Особенно акту­ально оно в период формирования многоукладной экономики. Измерение вариации, выяснение ее причины, выявление влияния отдельных факторов дает важную информацию (например, о про­должительности жизни людей, доходах и расходах населения, фи­нансовом положении предприятия и т.п.) для принятия научно обоснованных управленческих решений.

Средняя величина дает обобщающую характеристику при­знака изучаемой совокупности, но она не раскрывает строения совокупности, которое весьма существенно для ее познания. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Средняя величина при­знака в двух совокупностях может быть одинаковой, но в одном случае все индивидуальные значения отличаются от нее мало, а в другом — эти отличия велики, т.е. в одном случае вариация признака мала, а в другом — велика, это имеет весьма важное значение для характеристики надежности средней величины.

Чем больше варианты отдельных единиц совокупности различаются между собой, тем больше они отличаются от своем средней, и наоборот, — чем меньше варианты отличаются друг от друга, тем меньше они отличаются от средней, которая в тан ком случае будет более реально представлять всю совокупность. Вот почему ограничиваться вычислением одной средней в ряде случаев нельзя. Нужны и другие показатели, характеризующие отклонения отдельных значений от общей средней.

Это можно показать на таком примере. Предположим, что одинаковую работу выполняют две бригады, каждая — из трех человек. Пусть количество деталей, шт., изготовленных за смену отдельными рабочими, составляло:

в первой бригаде — 95, 100, 105 (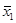= 100 шт.);

во второй бригаде — 75, 100, 125 ( 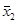= 100 шт.).

Средняя выработка на одного рабочего в обеих бригадах одинакова и составляет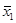= = 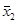100 шт., однако колеблемость выработки отдельных рабочих в первой бригаде значительно меньше, чем во второй.

Поэтому возникает необходимость измерять вариацию признака в совокупностях. Для этой цели в статистике применяют ряд обобщающих показателей.

Ø К показателям вариации относятся: размах вариации, сред­нее линейное отклонение, дисперсия и среднее квадратическое откло­нение, коэффициент вариации.

Ø Самым элементарным показателем вариации признака яв­ляется размах вариации R, представляющий собой разность между максимальным и минимальным значениями признака:

.

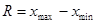В нашем примере размах вариации сменной выработки дета­лей составляет: в первой бригаде — R₁= 10 шт. (т.е. 105 — 95); во второй бригаде — R₂= 50 шт. (т.е. 125 — 75), что в 5 раз больше.

Это свидетельствует о том, что при численном равенстве средняя выработка первой бригады более «устойчива». Размах вариации может служить базой расчета возможных резервов роста выработки. Таких резервов больше у второй бригады, по­скольку в случае достижения всеми рабочими максимальной для этой бригады выработки деталей, ею может быть изготовлено 375 шт., т.е. (3x125), а в первой - только 315 шт., т.е. (3 х 105).

Однако размах вариации показывает лишь крайние отклоне­ния признака и не отражает отклонений всех вариантов в ряду. При изучении вариации нельзя ограничиваться только опреде­лением ее размаха. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и даёт обобщённую характеристику. Простейший показатель такого типа - среднее линейное отклонение

Ø Среднее линейное отклонение d представляет собой сред­нюю арифметическую абсолютных значений отклонений отдель­ных вариантов от их средней арифметической (при этом всегда предполагают, что среднюю вычитают из варианта: ().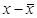

Среднее линейное отклонение:

Для несгруппированных данных , (5.18)

где n – число членов ряда;

Для сгруппированных данных , (5.19)

где 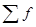— сумма частот вариационного ряда.

В формулах (5.18) и (5,19) разности в числителе взяты по модулю, (иначе в числителе всегда будет ноль — алгебраическая сумма отклонений вариантов от их средней арифметической). Поэтому среднее линейное отклонение как меру вариации при­знака применяют в статистической практике редко (только в тех случаях, когда суммирование показателей без учета знаков име­ет экономический смысл). С его помощью, например, анализи­руется состав работающих, ритмичность производства, оборот внешней торговли.

Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляет­ся по формулам простой и взвешенной дисперсий (в зависимо­сти от исходных данных):

§ простая дисперсия для несгруппированных данных

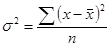, (5.20)

§ взвешенная дисперсия для вариационного ряда

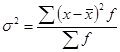. (5.20)

Формула (5.21) применяется при наличии у вариантов своих весов (или частот вариационного ряда).

Формулу для расчета дисперсии (5.20) можно преобразовать, учитывая, что

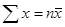
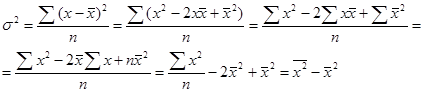
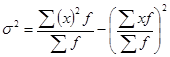(5.22)

т.е. дисперсия равна разности средней из квадратов вариан­тов и квадрата их средней.

Техника вычисления дисперсии по формулам (5.20), (5.21) достаточно сложна, а при больших значениях вариантов и час­тот может быть громоздкой.

Расчет можно упростить, используя свойства дис­персии (доказываемые в математической статистике). При­ведем два из них:

первое — если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия от этого не изменится;

второе — если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия соответст­венно уменьшится или увеличится в i² раз. Используя второе свойство дисперсии, разделив все вариан­ты на величину интервала, получим следующую формулу вы­числения дисперсии в вариационных рядах с равными интервалами по способу моментов:

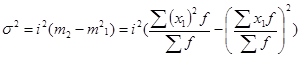(5.23)

где 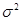— дисперсия, исчисленная по способу моментов;

i - величина интервала;

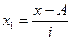новые (преобразованные) значения вариантов (А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой);

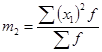- момент второго порядка;

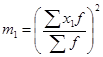- квадрат момента первого порядка.

Расчет дисперсии по формуле (5.23) менее трудоемок.

Дисперсия имеет большое значение в экономическом анали­зе. В математической статистике важную роль для характеристи­ки качества статистических оценок играет их дисперсия. Ниже, в частности, будет показано разложение дисперсии на соответст­вующие элементы, позволяющие оценить влияние различных факторов, обуславливающих вариацию признака; использование дисперсии для построения показателей тесноты корреляционной связи при оценке результатов выборочных наблюдений.

Ø Среднее квадратическое отклонение 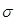равно корню квад­ратному из дисперсии:

§ для несгруппированных данных

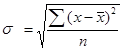, (5.24)

§ для вариационного ряда

. (5.25)

Среднее квадратическое отклонение — это обобщающая ха­рактеристика размеров вариации признака в совокупности; оно показывает, на сколько в среднем отклоняются конкретные ва­рианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.

Обозначим: 1 — наличие интересующего нас признака; 0 — его отсутствие; р — доля единиц, обладающих данным признаком; q — доля единиц, не обладающих данным признаком; p + q =1. Исчислим среднее значение альтернативного признака иего дисперсию. Среднее значение альтернативного признака

, (5.26)

так как р + q = 1.

Дата добавления: 2014-01-06