Распределение урожайности по хозяйствам региона, имеющим различную форму собственности

Хозяйства (по формам собственности)	Количество обследованных хозяйств f	Средняя урожайность, ц/га xi	Дисперсия уро­жайности в ка­ждой группе Si^2
Коллективные Акционерные обще­ства Крестьянские (фермерские)
Итого		–	–

Решение. Поскольку обследованные хозяйства региона сгруппи­рованы по формам собственности, предельную ошибку средней урожайности определяем по формуле для типической выборки, осуществляемой методом повторного отбора (численность гене­ральной совокупности N неизвестна):

.

В этой формуле неизвестна средняя из внутригрупповых дис­персий.

Она исчисляется по формуле:

.

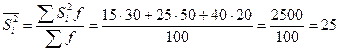По представленным ранее данным Ф(t) для вероятности Р=0,954 находим t=2.

Тогда предельная ошибка выборки, ц/га:

.

Генеральная средняя . Для нахождения ее границ вначале нужно исчислить среднюю урожайность по выборочной совокупности , ц/га:

.

Предельная относительная ошибка выборки, %:

.

Доверительные пределы генеральной средней исчисляем, исхо­дя из двойного неравенства:

;

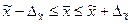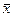21-1≤≤21+1; 20≤≤22.

Таким образом, с вероятностью 0,954 можно гарантировать, что средняя урожайность зерновых культур по региону будет не менее чем 20 ц/га, но и не более чем 22 ц/га.

Определение необходимого объема выборки. При проектирова­нии выборочного наблюдения с заранее заданным значением допустимой ошибки выборки очень важно правильно опреде­лить численность (объем) выборочной совокупности, которая с определенной вероятностью обеспечит заданную точность ре­зультатов наблюдения. Формулы для определения необходимой численности выборки п легко получить непосредственно из формул ошибок выборки.

Так, из формул предельной ошибки выборки для повтор­ного отбора нетрудно (предварительно возведя в квадрат обе части равенства) выразить необходимую численность выборки:

• для средней количественного признака

; (6.29)

• для доли (альтернативного признака)

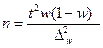. (6.30)

Аналогично из формул предельной ошибки выборки для бесповторного отбора находим, что

(для средней); (6.31)

(для доли). (6.32)

Эти формулы показывают, что с увеличением предполагае­мой ошибки выборки значительно уменьшается необходимый объем выборки.

Для расчета объема выборки нужно знать дисперсию. Она может быть заимствована из проводимых ранее обследований данной или аналогичной совокупности, а если таковых нет, то­гда для определения дисперсии надо провести специальное вы­борочное обследование небольшого объема.

Задача 4. Для определения среднего возраста 1200 студентов факультета необходимо провести выборочное обследование мето­дом случайного бесповторного отбора. Предварительно установле­но, что среднее квадратическое отклонение возраста студентов рав­но 10 годам.

Сколько студентов нужно обследовать, чтобы с вероятно­стью 0,954 средняя ошибка выборки не превышала 3 года?

Решение. Рассчитаем необходимую численность выборки, чел., по формуле бесповторного отбора (6.31), учитывая, что t= 2 при Р= 0,954:

.

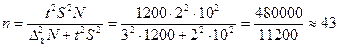Таким образом, выборка численностью 47 чел. обеспечивает задан­ную точность при бесповторном отборе.

Выборочный метол широко используется в статистической практике для получения экономической информации.

Большую актуальность приобретает выборочный метод в со­временных условиях перехода к рыночной экономике. Изменения в характере экономических отношений, аренда, собственность от­дельных коллективов и лиц обусловливают изменения функций учета и статистики, сокращение и упрощение отчетности. Вместе с тем, возрастающие требования к менеджменту усиливают потреб­ность в обеспечении надежной информацией, дальнейшего повы­шения ее оперативности. Все это обусловливает более широкое применение выборочного метода в экономике.

В отечественной статистике уже накоплен определенный опыт выборочных обследований. В последние годы все большее применение в социальной статистике находят специальные вы­борочные наблюдения. Так, важнейшим источником информа­ции об уровне жизни народа являются данные регулярно прово­димых выборочных обследований бюджетов семей. Широко применяется выборочный метод при переписи населения, изу­чении общественного мнения, контрольных обходах и провер­ках после проведения сплошных обследований.

Потребность в использовании выборочного метода, выра­ботке вероятностных суждений в современной отечественной статистике непрерывно расширяется.

Контрольные вопросы

1. Какое наблюдение называется выборочным?
2. В чем преимущества выборочного наблюдения перед сплошным?
3. Какие вопросы необходимо решить для проведения выбороч­ного наблюдения?
4. Почему при выборочном наблюдении неизбежны ошибки и как они классифицируются?
5. Каковы условия правильного отбора единиц совокупности при выборочном наблюдении?
6. Как производятся собственно-случайный, механический, типический и серийный отборы?
7. В чем различие повторной и бесповторной выборки?
8. Что представляет собой средняя ошибка выборки (для средней и доли)?
9. По каким расчетным формулам находят средние ошибки выборки (для средней и доли) при повторном и беспо­вторных отборах?
10. Что характеризует предельная ошибка выборки и по каким формулам она исчисляется (для средней и доли)?
11. Что показывает коэффициент доверия?
12. В чем значение теоремы Чебышева — Ляпунова для решения задач выборочного наблюдения?
13. Какими способами осуществляется распространение ре­зультатов выборочного наблюдения на всю совокупность?
14. Зачем и как исчисляются предельные статистические ошибки выборки (для средней и доли)?
15. По каким формулам определяется необходимая численность выборки, обеспечивающая с определенной вероятностью за­данную точность наблюдения?

Глава 7. Статистическое изучение динамики

7.1. Понятие о рядах динамики

Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, т. е. их ди­намика. Эта задача решается при помощи анализа рядов динами­ки (или временных рядов).

Ряд динамики (или динамический ряд) представляет собой ряд расположенных в хронологической последовательности чи­словых значений статистического показателя, характеризующих изменение общественных явлений во времени.

В каждом ряду динамики имеются два основных элемента: время t и конкретное значение показателя (уровень ряда) у.

Уровни ряда – это показатели, числовые значения которых составляют динамический ряд. Время – это моменты или перио­ды, к которым относятся уровни.

Построение и анализ рядов динамики позволяют выявить и измерить закономерности развития общественных явлений во времени. Эти закономерности не проявляются четко на каждом конкретном уровне, а лишь в тенденции, в достаточно дли­тельной динамике. На основную закономерность динамики на­кладываются другие, прежде всего случайные, иногда сезонные влияния. Выявление основной тенденции в изменении уров­ней, именуемой трендом, является одной из главных задач ана­лиза рядов динамики.

По времени, отраженному в динамических рядах, они разде­ляются на моментные и интервальные.

Моментным рядом динамики называется такой ряд, уровни которого характеризуют состояние явления на определенные да­ты (моменты времени).

Примером моментного ряда могут служить следующие дан­ные о численности населения.

Численность постоянного населения РФ (на 1 января), млн. чел.:

1992 г. 1993 г. 1994 г. 1995 г. 1996 г. 1997 г. 1998 г. 1999 г.

148,3 148,3 147,9 147,94 147,6 147,1 146,7 146,3

Источник: Российской статистический ежегодник. — М., 1999. — С.53.

Этот ряд характеризует динамику численности населения России в 1993-1999 гг.

Поскольку в каждом последующем уровне содержится пол­ностью или частично значение предыдущего уровня, суммиро­вать уровни моментного ряда не следует, так как это приводит к повторному счету.

Интервальным (периодическим) рядом динамики называется такой ряд, уровни которого характеризуют размер явления за конкретный период времени (год, квартал, месяц). Примером такого ряда могут служить данные о динамике добычи нефти в Российской Федерации.

Добыча нефти в Российской Федерации, млн. т:

1991г. 1992 г. 1993 г. 1994 г. 1993 г. 1996 г. 1997 г. 1998 г.

462 399 354 318 307 301 306 303

Источник: Российский статистический ежегодник. — М., 1999. — С.53.

Этот ряд характеризует снижение уровня добычи нефти в России.

Значения уровней интервального ряда в отличие от уровней моментного ряда не содержатся в предыдущих или последую­щих показателях, их можно просуммировать, что позволяет по­лучать ряды динамики более укрупненных периодов. Например, суммирование уровней добычи нефти за каждый год по данным, приведенным выше, позволяет определить ее добычу за все восемь лет в целом и в среднем за год.

Интервальный ряд, где последовательные уровни могут суммироваться, можно представить как ряд с нарастающими итогами. При построении таких рядов производится последовательное суммирование смежных уровней. Этим достигается суммар­ное обобщение результата развития изучаемого явления с начала отчетного периода (месяца, квартала, года и т.д.).

Уровни в динамическом ряду, могут быть представлены абсолютными, средними или относительными величинами. Так, в рассмотренных рядах динамики уровни выражены абсолютными статистическими величинами. Средними величинами могут вы­ражаться уровни, характеризующие динамику средней реальной заработной платы в промышленности, динамику урожайности зерновых культур (ц/га). Относительными величинами характе­ризуются, например, динамика доли городского и сельского на­селения (%) и уровня безработицы.

По расстоянию между уровнями ряды динамики подразде­ляются на ряды с равностоящими и неравностоящими уровнями по времени. Например, ранее приведенные данные о добыче нефти в Российской Федерации за 1991 — 1998 гг. представляют собой ряд динамики с равностоящими уровнями (объемы до­бычи нефти представлены через равные, следующие друг за другом интервалы времени).

Если в рядах динамики прерывающиеся или неравномерные интервалы времени, то такие ряды являются неравностоящими.

Ряды динамики могут быть изображены графически. Графиче­ское изображение позволяет наглядно представить развитие явления во времени и способствует проведению анализа уровней. Наиболее распространенным видом графического изображения для аналити­ческих целей является линейная диаграмма, которая строится в прямоугольной системе координат: на оси абсцисс отмечается время, а на оси ординат — уровни ряда (рис. 7.1).

Рис. 7.1. Динамика численности студентов (на 10 тыс. населения)

Источник: Российский статистический ежегодник. — М., 1999. — С. 196,201.

Наряду с линейной диаграммой для графического изобра­жения рядов динамики в целях популяризации широко исполь­зуются столбиковая диаграмма (рис. 7.2), секторная диаграмма (рис. 7.3) и другие виды диаграмм (фигурные, квадратные, по­лосовые и т.п.).

1990 1991 1992 1993 1994 1995 1996 1997 1998

Рис. 7.2. Конкурс на вступительных экзаменах в государственных высших учебных заведениях РФ (на одного зачисленного приходится державших экзамены)

Источник: Российский статистический ежегодник. — М., 1999. — С. 207.

Рис. 7.3. Структура фактического конечного потребления продуктов домашних хозяйств:

█ -покупка товаров и оплата услуг;

█ -социальные трансферты в натуральной форме;

█ -поступление товаров и услуг в натуральной форме.

Источник: Российский статистический ежегодник. — М., 1999. — С. 142.

7.2. Правила построения рядов динамики

При построении динамических рядов необходимо соблюдать определенные правила: основным условием для получения правильных выводов при анализе рядов динамики и прогнозировании его уровней является сопоставимость уровней динамического ряда между собой.

Статистические данные должны быть сопоста­вимы по территории, кругу охватываемых объектов, единицам изме­рения, времени регистрации, ценам, методологии расчета и др.

Ø Сопоставимость по территории предполагает одни и те же границы территории. Вопрос о том, является ли это требо­вание непременным условием сопоставимости уровней дина­мического ряда, может решаться по-разному, в зависимости от целей исследования. Так, при характеристике роста экономи­ческой мощи страны следует использовать данные в имеющих­ся границах территории, а при изучении темпов экономиче­ского развития следует брать данные по территории в одних и тех же границах. Объясняется это тем, что изменение границ влияет на численность населения, объем продукции.

Ø Сопоставимость по кругу охватываемых объектов означа­ет сравнение совокупностей с равным числом элементов.

При этом нужно иметь в виду, что сопоставляемые показате­ли динамического ряда должны быть однородны по экономиче­скому содержанию и границам объекта, который они характеризуют (однородность может быть обеспечена одинаковой полно­той охвата разных частей явления). Например, при характеристи­ке динамики численности студентов высших учебных заведений по годам нельзя в одни годы учитывать только численность сту­дентов дневного обучения, а в другие - численность студентов всех видов обучения. Несопоставимость может возникнуть вслед­ствие перехода ряда объектов (например, предприятий отрасли) из одного подчинения в другое. Однако сопоставимость не нару­шается, если в отрасли в строй введены новые предприятия или отдельные предприятия прекратили работу.

Ø Сопоставимость по времени регистрации для интер­вальных рядов обеспечивается равенством периодов времени, за которые приводятся данные. Нельзя, например, при изуче­нии ритмичности работы предприятия сравнивать данные об удельном весе продукции по определенным декадам, так как число рабочих дней отдельных декад может оказаться существенно различным, что приводит к различиям в объеме выпус­ка продукции. Это относится и к рядам внутригодовой дина­мики с месячными, квартальными уровнями. Для приведения таких рядов динамики к сопоставимому виду исчисляют среднедневные показатели по декадам, месяцам, кварталам, которые затем сопоставляют, сравнивают.

Для моментных рядов динамики показатели следует приво­дить на одну и ту же дату. Так, переоценку в сопоставимые цены основных фондов по отраслям экономики в условиях высокой инфляции нужно производить ежегодно по состоянию на 1 января. Или другой пример: если учет численности скота в те­чение ряда лет проводился по состоянию на 1 октября, а затем — на 1 января, то соединение в один ряд показателей (за несколько лет) с разной датой учета даст несопоставимые уровни (числен­ность скота осенью обычно больше, чем зимой).

Ø Сопоставимость по ценам. При проведении к сопостави­мому виду продукции, измеренной в стоимостных (ценностных) показателях, трудность заключается в том, что, во-первых, с те­чением времени происходит непрерывное изменение цен, а во-вторых, существует несколько видов цен. Для характеристики изменения объема продукции должно быть устранено (элими­нировано) влияние изменения цен. Поэтому на практике коли­чество продукции, произведенной в разные периоды, оценивают в ценах одного и того же базисного периода, которые называют неизменными, или сопоставимыми ценами.

Ø Сопоставимость по методологии расчета. Приопределе­нии уровней динамического ряда необходимо использовать еди­ную методологию их расчета. Например, в одни годы среднюю урожайность рассчитывали с засеянной площади, а в другие — с убранной. До 1958 г. уровень производительности труда в про­мышленности определялся в расчете на одного рабочего, а с 1958 г. — на одного работающего (т. е. с включением подсобных рабочих, ИТР и служащих). Поэтому для динамического анали­за уровни производительности труда, рассчитанные до 1958 г., необходимо пересчитывать по новой методологии.

Нередко статистические данные выражаются в различных единицах измерения. С этим часто приходится сталкиваться при учете продукции в натуральном выражении. Например, данные о количестве произведённого молока могут быть выражены в литрах и килограммах. Для того, чтобы обеспечить сравнимость такого ряда данных, необходимо выразить их в одних и тех же единицах измерения, т. е. или только в литрах, или только в ки­лограммах (то же для валового сбора зерна — пуды и тонны).

Вполне очевидна несопоставимость денежных единиц разных стран, несопоставимость денежных единиц внутри одной страны за разные периоды времени (при изменении курса валюты).

Могут быть и другие причины несопоставимости уровней рядов динамики.

Рассмотренные примеры показывают, что часто приходится иметь дело с такими несопоставимыми данными, которые могут быть при­ведены к сопоставимому виду дополнительными расчетами.

В ряде случаев несопоставимость может быть устранена пу­тем обработки рядов динамики приемом, который носит назва­ние смыкание рядов динамики. Этот прием позволяет преодолеть несопоставимость данных, возникающую вследствие изменения во времени круга охватываемых объектов или методологии рас­чета показателей, и получить единый сравнимый ряд за весь пе­риод времени. Если, например, имеются два ряда показателей, характеризующих динамику одного и того же явления в новых и старых границах по одному и тому же кругу объектов, то такие динамические ряды можно сомкнуть.

Пусть, например, имеются следующие данные об объеме реализации продукции фирмы «Весна» (название условное), в которую до 1996 г. входило 10 предприятий, а с 1996 г. — 12 предприятий (табл.7.1).

Необходимо получить единый ряд, который был бы приго­ден для характеристики динамики объема реализации продук­ции за весь рассматриваемый период.

Показатели за 1996—1999 гг. не сопоставимы непосредствен­но с показателями за 1993—1995 гг., так как относятся к раз­личному количеству предприятий. Задача заключается в ис­числении данных за 1993-1995 гг. в новых границах (по но­вому числу предприятий), ее решение осуществляется смыканием рядов. Для этого по данным 1996 г. исчисляем коэффициент со­отношения уровней двух рядов: k = 168 / 140 = 1,20.

Таблица 7.1.

Динамика объема реализации продукции фирмы «Весна» в сопоставимых ценах, млн. руб. (по годам)

Объем реализации	1993 г.	1994 г.	1995 г.	1996 г.	1997 г.	1998 г.	1999 г.
Продукция 10 предприятий Продукция 12 предприятий	–	–	–		–	–	–
Сопоставимый ряд

Умножая на этот коэффициент уровни первого ряда, полу­чаем скорректированные данные за 1993—1995 гг. в новых гра­ницах, млн. руб.:

У₁₉₉₃ = 120 *1,20 = 144,0;

У₁₉₉₄ = 125*1,20 = 150,0;

У₁₉₉₅=130*1,20 = 156,0.

Сомкнутый сопоставимый ряд представлен в табл. 7.1. Смы­кание рядов дает возможность устранить несопоставимость уровней и получить представление о динамике за весь период. Однако при этом следует иметь в виду, что результаты, полу­ченные путем смыкания рядов, являются приближенными, т. е. содержат некоторую погрешность.

Таким образом, прежде чем анализировать динамические ряды, следует убедиться в сопоставимости их уровней и, если сопоставимость отсутствует, добиться ее дополнительными рас­четами, когда это возможно.

7.3. Показатели анализа ряда динамики

При изучении динамики общественных явлений возникает проблема описания интенсивности изменения и расчета средних показателей динамики.

Анализ интенсивности изменения во времени осуществляет­ся с помощью показателей, получаемых в результате сравнения уровней, к таким показателям относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процен­та прироста.

Система средних показателей включает средний уровень ря­да, средний абсолютный прирост, средний темп роста, средний темп прироста.

Показатели анализа динамики могут вычисляться на посто­янной и переменных базах сравнения. При этом принято назы­вать сравниваемый уровень отчетным, а уровень, с которым производится сравнение, — базисным.

Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же ба­зисным уровнем. В качестве базисного выбирается либо началь­ный уровень в ряду динамики, либо уровень, с которого начи­нается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными.

Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с преды­дущим. Вычисленные таким образом показатели анализа дина­мики называются цепными.

Важнейшим статистическим показателем анализа динамики яв­ляется абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за оп­ределенный промежуток времени. Абсолютный прирост с пере­менной базой называют скоростью роста.

Абсолютный прирост Абсолютный прирост

(цепной): (базисный):

; (7.1, a) ; (7.1,б)

где у_i — уровень сравниваемого периода;

y_i-1 — уровень предшествующего периода;

y₀ ^— уровень базисного периода.

Цепные и базисные абсолютные приросты представлены в табл. 7.2. Они показывают прирост (сокращение) производства электроэнергии РФ по годам и абсолютное изменение по срав­нению с 1992 г.

Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток вре­мени ().

По данным табл. 7.2 сумма последовательных цепных абсо­лютных приростов равна базисному приросту за весь период:

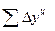= -81 -16-13-13 -7 = -130.

Для оценки интенсивности, т. е. относительного изменения уровня динамического ряда за какой-либо период времени ис­числяют темпы роста (снижения).

Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному.

Показатель интенсивности изменения уровня ряда, выра­женный в долях единицы, называется коэффициентом роста, а в процентах — темпом роста. Эти показатели интенсивности из­менения отличаются только единицами измерения.

Таблица 7.2

Динамика производства электроэнергии в Российской Федерации

Год	Производство электроэнергии, млрд. кВт*ч	Абсолютный прирост, млрд. кВт. ч	Коэффициенты роста	Темпы прироста, %	А%	Пункты роста (сниже­ния), %
1	2	3	4	5	6		8	9	10
		–   876-957= -81 860-876=16 -13 -13 - 7	–   876-957=-81 860-957= -97 -110 -123 -130	– 0,985 0,985 0,992	– 0.885 0,871 0,864	–   91,5-100= -8,5 -1,8 -1,5 -1,5 -0,8	–   91,5-100 = -8,5 -10,3 -11,5 -12,9 -13,6	–   9,57 8.76 8,60 8,47 8,34	– - 8,5 -1,8 -1,2 -1,4 -0,7
Итого: 5201	∑=-130	–	∏ = 0,864	–	–	–	–	∑=-13,6
Примечания: 1) в графе 1- сравнение с уровнем предшествующего года; в графе 2 - с уровнем 1993 г.; 2) - абсолютное значение 1% прироста, млрд. кВт *ч.

Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым произ­водится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.

Коэффициент роста: Коэффициент роста:

(цепной) (базисный)

(7.2, а) . (7.2,б)

Темп роста (цепной): Темп роста (базисный):

, (7.3, a) . (7.3, б)

Итак, Т_р = К_р * 100.

Цепные и базисные коэффициенты роста, характеризующие интенсивность изменения производства электроэнергии в Рос­сии по годам и за весь период, исчислены в табл. 7. 2.

Между цепными и базисными коэффициентами роста суще­ствует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведе­ние последовательных цепных коэффициентов роста равно базис­ному коэффициенту роста за весь период (), а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.

Взаимосвязь легко проверить: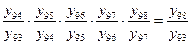

Проверим взаимосвязь цепных и базисных темпов роста на нашем примере:

∏ = 0,915 * 0,982 * 0,985 * 0,985*0,992 = 0,864.

Относительную оценку скорости измерения уровня ряда в еди­ницу времени дают показатели темпа прироста (сокращения).

Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения, и вычисляется как отношение абсолютного при­роста к абсолютному уровню, принятому за базу сравнения.

Темп прироста может быть положительным, отрицательным или равным нулю, выражается он в процентах и долях единицы (коэффициенты прироста).

Темп прироста (цепной): Темп прироста (базисный):

; (7.4, а) (7.4, б)

Темп прироста (сокращения) можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста получается вычитанием единицы из коэффициента роста:

Т_пр = Т_р - 100; (7.5, а) К_пр = К_р - 1. (7.5,б)

Цепные и базисные темпы прироста (сокращения) произ­водства электроэнергии исчислены в табл. 7.2.

При анализе динамики развития следует также знать, какие абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при снижении (замедле­нии) темпов прироста абсолютный прирост не всегда уменьша­ется, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени, %:

(7.6)

Абсолютное значение одного процента прироста равно сотой части предыдущего (или базисного) уровня. Оно показывает, какое абсолютное значение скрывается за относительным пока­зателем - одним процентом прироста.

Абсолютные значения 1% прироста исчислены в табл. 7.2. Дан­ные показывают, что абсолютное значение 1% прироста производ­ства электроэнергии в России в 1993-1999 гг. снижалось.

В тех случаях, когда сравнение производится с отдалением периода времени, принятого за базу сравнения, рассчитывают так называемые пункты роста, которые представляют собой разность базисных темпов роста, %, двух смежных периодов.

В отличие от темпов прироста, которые нельзя ни суммиро­вать, ни перемножать, пункты роста можно суммировать, в ре­зультате получаем темп прироста соответствующего периода по сравнению с базисным. По данным табл. 7.2, сумма пунктов роста равна - 13,6%, что соответствует темпу прироста уровня изучаемого показателя в 1998 г. по сравнению с 1993 г.

Для более глубокого понимания характера явления необходимо показатели динамики анализировать комплексно, совместно.

Для обобщающей характеристики динамики исследуемого явления определяют средние показатели: средние уровни ряда и средние показатели изменения уровней ряда.

Ø Средний уровень ряда характеризует обобщённую вели­чину абсолютных уровней. Он рассчитывается по средней хро­нологической, т. е. по средней исчисленной из значений, изме­няющихся во времени.

Методы расчета среднего уровня интервального и моментного рядов динамики различны.

Для интервальных рядов динамики из абсолютных уровней средний уровень за период времени определяется по формуле средней арифметической:

§ при равных интервалах применяется средняя арифметиче­ская простая:

; (7.7)

где y – абсолютные уровни ряда, n – число уровней ряда.

§ при неравных интервалах- средняя арифметическая взвешенная

; (7.8)

где y₁,…,y_n – уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени t;

t₁,…,t_n – веса, длительность интервалов времени (дней, месяцев) между смежными датами.

Средний уровень производства электроэнергии за 1993— 1998 гг. находим по формуле (7.6), так как исследуемый ряд динамики представляет собой интервальный ряд с одинаковыми интервалами, млрд. кВт. ч:

Расчет среднего уровня для интервального ряда динамики с неравностоящими уровнями рассмотрим на примере.

Пример. Если известно, что с 1-го по 15-е число месяца в ак­ционерном коммерческом банке работали 20 человек, с 16-го по 25-е - 27 человек, а с 26-го по 30-е - 30 человек, то среднесписоч­ное число работников за месяц составит, чел.:

Средний уровень моментного ряда динамики с равностоящими уровнями определяется по формуле средней хронологической мо­ментного ряда:

; (7.9)

где y₁…y_n - уровни периода, за который делается расчет;

п - число уровней;

п - 1 - длительность периода времени.

Пример. Пусть имеются данные о валютном курсе, установ­ленном ЦБ РФ первое число каждого месяца.

Котировка доллара США, руб. за 1 долл.:

1. X. 1999 г. 1. XI. 1999 г. 1. XII. 1999 г. 1. 1.2000 г.

25.05 26,05 26,75 27,0

Требуется определить средний месячный курс доллара в IV квартале 1999 г.

Так как t₁ = t₂ = t₃ = t₄, для расчета применяем формулу (7.8), руб./долл.:

Средний уровень моментных рядов с неравностоящими уровнями определяется по формуле средней хронологической взвешенной:

(7.10)

где у_i,у_п - уровни рядов динамики; t - интервал времени между смежными уровнями.

Использование в расчетах формулы (7.10) рассмотрим на следую­щем примере.

Масса остатков (запасов) дизельного топлива в фермерском хозяйстве, т:

1.1.1999 г. 1.111.1999 г. 1. IV. 1999 г. 1. VIII 1999 г. 1.1.2000 г.

40 60 100 10 30

Нужно определить среднюю массу остатков (запасов) дизельного топлива в фермерском хозяйстве за 1999 г., т:

Ø Обобщающий показатель скорости изменения уровней во времени — средний абсолютный прирост (убыль), представляющий собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний абсолютный при­рост как среднюю арифметическую простую:

(7.11)

где п - число цепных абсолютных приростов в изучаемом периоде.

Применение формулы (7.11) проиллюстрируем, используя данные табл. 7.2 о цепных абсолютных приростах производства электроэнергии, млрд. кВт. ч:

.

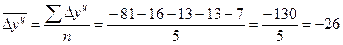Средний абсолютный прирост определим через накопленный (базисный) абсолютный прирост ( ). Для случая равных ин­тервалов применим следующую формулу:

(7.12)

где т — число уровней ряда динамики в изучаемом периоде, включая базисный.

Для нашего примера, млрд. кВт * ч: т. е. получен тот же результат.

Ø Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста (снижения), показывающий, во сколько раз в среднем за едини­цу времени изменяется уровень ряда динамики.

Средний темп роста (снижения) — обобщенная характеристика индивидуальных темпов роста ряда динамики. В качестве основы и критерия правильности исчисления среднего темпа роста (сни­жения) применяется определяющий показатель — произведение цепных темпов роста, равное темпу роста за весь рассматривае­мый период. Следовательно, если значение признака образуется как произведение отдельных вариантов, то согласно общему пра­вилу (см. гл.5.1.) нужно применять среднюю геометрическую.

Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах (), то для равностоящих рядов динамики расчеты по средней геомет­рической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):

, (7.13)

где п - число цепных коэффициентов роста;

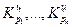- цепные коэффициенты роста; 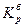- базисный ко­эффициент роста за весь период.

В нашем примере среднегодовой темп изменения производ­ства электроэнергии с 1994 по 1998 гг.:

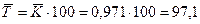т.е. 97,1%

Следовательно, с 1994 по 1999 гг. производство электро­энергии в России снижалось в среднем на 2,9% в год, т. е. (0,971 * 100 - 100).

Если известны уровни динамического ряда, то расчет сред­него коэффициента роста упрощается. Так как произведение цепных коэффициентов роста равно базисному, то в подкорен­ное выражение подставляется базисный коэффициент роста. Ба­зисный коэффициент, как известно, получается непосредственно как частное от деления уровня последнего периода у„ на уровень базисного периода у₀.

Тогда формула для расчета среднего коэффициента роста для равностоящих рядов динамики (по «базисному способу»):

, (7.14)

где т — число уровней ряда динамики в изучаемом периоде, вклю­чая базисный.

Для расчета средних коэффициентов роста по формуле (7.14) не нужно знать годовые темпы. Для нашего примера:

.

Получен тот же результат, расчеты упрощены.

Ø Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста, вычитанием из последних 100 %. Соответственно при исчислении средних коэффициентов прироста из значений коэффициентов роста вычитается единица:

; ,

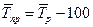где — средний темп прироста, — средний коэффициент прироста

Если уровни ряда динамики снижаются, то средний темп роста будет меньше 100%, а средний темп прироста — отрица­тельной величиной. Отрицательный темп прироста пред­ставляет собой средний темп сокращения и характеризует сред­нюю относительную скорость снижения уровня.

Так, в нашем примере среднегодовой темп прироста произ­водства электроэнергии характеризуется отрицательным значе­нием (-2,9%), что свидетельствует о ежегодном сокращении производства электроэнергии.

При анализе развития явлений, отражаемых двумя динамиче­скими рядами, представляет интерес сравнение интенсивностей изменения во времени обоих явлений. Такое сопоставление интенсивностей изменения производится при сравнении динамиче­ских рядов одинакового содержания, но относящихся к разным территориям (странам, республикам, районам и т.п.), или к раз­личным организациям (министерствам, предприятиям, учрежде­ниям), или при сравнении рядов разного содержания, но харак­теризующих один и тот же объект. Например, сравнение рядов динамики, характеризующих производство важнейших видов продукции в Российской Федерации и других странах.

Сравнительные характеристики направления и интенсивно­сти роста одновременно развивающихся во времени явлений определяются приведением рядов динамики к общему (единому) основанию и расчетом коэффициентов опережения (отставания).

Ø Ряды динамики (в которых возникают, например, про­блемы сопоставимости цен сравниваемых стран, методики рас­чета сравниваемых показателей и т.п.) обычно приводят к одно­му основанию, если они не могут быть решены другими метода­ми. По исходным уровням нескольких рядов динамики опреде­ляют относительные величины - базисные темпы роста или прироста. Принятый при этом за базу сравнения период време­ни (дата) выступает в качестве постоянной базы расчетов тем­пов роста для каждого из изучаемых рядов динамики. В зависи­мости от целей исследования базой может быть начальный, средний или другой уровень ряда.

Таблица 7.3

Дата добавления: 2014-01-06