Понятие средней арифметической

Виды средних величин отличают, прежде всего, тем, какое свойство, какой параметр исходной варьирующей массы индивидуальных значений признака должен быть сохранен неизменным.

Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным.

Иначе можно сказать, что средняя величина - среднее слагаемое. При её вычислении общий объем признака медленно распределяется поровну между всеми единицами совокупности. Например, средняя заработная плата или средний доход работников предприятия - это такая сумма денег, которая приходилась бы на каждого работника, если бы весь фонд заработной оплаты труда (или все доходы, направленные на личное потребление) был распределен между работниками поровну.

Исходя из определения, формула средней арифметической величины имеет вид:

(1)

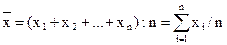
где 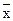- средняя величина;

n - численность совокупности

По формуле (1) вычисляются средние величины первичных признаков, если известны индивидуальные значения признака. Если изучаемая совокупность велика, исходная информация чаще представляет собой ряд распределения или группировку, например

Распределение футбольных матчей высшей лиги России по числу забитых за матч обеими командами мячей в 1996 г.

Число забитых мячей, х											Итого
Число матчей, fi

Среднее число мячей, забитых за одну игру, должно представлять собой результат равномерного распределения общего числа забитых мячей по всем 306 матчам розыгрыша первенства. Общее число забитых мячей можно получить как сумму произведений значений признака в каждой группе х, на число игр с таким количеством забитых мячей f_i (частоты или веса). Получим формулу (2):

(2)

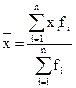
где n - число групп.

Такую форму средней величины называют взвешенной средней арифметической в отличии от простой средней, рассчитанной по формуле (1). В качестве весов выступают здесь числа единиц совокупности в разных группах. Название "вес" выражает тот факт, что разные значения признака имеют неодинаковую "важность" при расчете средней. Важнее число забитых мячей, которое встречалось чаще: 1, 2, 3 мяча, а такие значения, как 7 или 9 забитых мячей, как бы ни радовали болельщиков, при расчете средней не играют большой роли: их "вес" мал.

Таким образом имеем: 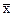= 802: 306 = 2,62 мяча за игру.

Как видим средняя арифметическая величина может быть дробным числом, если даже индивидуальные значения признака могут принимать только целые значения. Из определения средней величины не вытекает, что она обязательно должна быть реальным значением признака, которое могло встретиться у какой-либо единицы совокупности.

Дата добавления: 2014-01-06