Формула БАЙЕСА

При выводе формулы полной вероятности предполагалось, что событие А, вероятность которого следовало определить, могло произойти с одним из событий Н ₁ , Н ₂ ,..., Н_n, образующих полную группу попарно несовместных событий. При этом вероятности указанных событий (гипотез) были известны заранее. Предположим, что произведен эксперимент, в результате которого событие А наступило. Эта дополнительная информация позволяет произвести переоценку вероятностей гипотез Н_i, вычислив Р(Н_i/А).

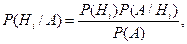
или, воспользовавшись формулой полной вероятности, получим

Эту формулу называют формулой Байеса или теоремой гипотез. Формула Байеса позволяет «пересмотреть» вероятности гипотез после того, как становится известным результат опыта, в результате которого появилось событие А.

Вероятности Р(Н_i) − это априорные вероятности гипотез (они вычислены до опыта). Вероятности же Р(Н_i/А) − это апостериорные вероятности гипотез (они вычислены после опыта). Формула Байеса позволяет вычислить апостериорные вероятности по их априорным вероятностям и по условным вероятностям события А.

Пример. Известно, что 5 % всех мужчин и 0.25 % всех женщин дальтоники. Наугад выбранное лицо по номеру медицинской карточки страдает дальтонизмом. Какова вероятность того, что это мужчина?

Решение. Событие А – человек страдает дальтонизмом. Пространство элементарных событий для опыта – выбран человек по номеру медицинской карточки – Ω = { Н ₁ , Н ₂ } состоит из 2 событий:

Н ₁ −выбран мужчина,

Н ₂ −выбрана женщина.

Эти события могут быть выбраны в качестве гипотез.

По условию задачи (случайный выбор) вероятности этих событий одинаковые и равны Р(Н ₁ ) = 0.5; Р(Н ₂ ) = 0.5.

При этом условные вероятности того, что человек страдает дальтонизмом, равны соответственно:

Р(А/Н ₁ ) = 0.05 = 1/20; Р(А/Н ₂ ) = 0.0025 = 1/400.

Так как известно, что выбранный человек дальтоник, т. е. событие произошло, то используем формулу Байеса для переоценки первой гипотезы:

Пример. Имеются три одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором – 10 белых и 10 черных, в третьем – 20 черных шаров. Из выбранного наугад ящика вынули белый шар. Вычислить вероятность того, что шар вынут из первого ящика.

Решение. Обозначим через А событие – появление белого шара. Можно сделать три предположения (гипотезы) о выборе ящика: Н ₁, Н ₂, Н ₃ − выбор соответственно первого, второго и третьего ящика.

Так как выбор любого из ящиков равновозможен, то вероятности гипотез одинаковы:

Р(Н ₁ )=Р(Н ₂ )=Р(Н ₃ )= 1/3.

По условию задачи вероятность извлечения белого шара из первого ящика

Вероятность извлечения белого шара из второго ящика

Вероятность извлечения белого шара из третьего ящика

Искомую вероятность находим по формуле Байеса:

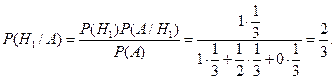
Повторение испытаний. Формула Бернулли.

Проводится n испытаний, в каждом из которых событие А может произойти или не произойти, причем вероятность события А в каждом отдельном испытании постоянна, т.е. не меняется от опыта к опыту. Как найти вероятность события А в одном опыте мы уже знаем.

Представляет особый интерес вероятность появления определенного числа раз (m раз) события А в n опытах. подобные задачи решаются легко, если испытания являются независимыми.

Опр. Несколько испытаний называюся независимыми относительно события А, если вероятность события А в каждом из них не зависит от исходов других опытов.

Вероятность Р_n(m) наступления события А ровно m раз (ненаступление n-m раз, событие ) в этих n испытаниях. Событие А появляется в самых разных последовательностях m раз).

- формулу Бернулли.

Очевидны следующие формулы:

Р_n(m<k) = Р_n(0) + Р_n(1) +…+ Р_n(k-1) - вероятность наступления события А менее k раз в n испытаниях.

P_n(m>k) = P_n(k+1) + P_n(k+2) +…+ P_n(n) - вероятность наступления события А более k раз в n испытаниях.

P_n(mk) = P_n(k) + P_n(k+1) + P_n(k+2) +…+ P_n(n) - вероятность наступления события А не менее k раз в n испытаниях

Р_n(m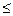k) = Р_n(0) + Р_n(1) +…+ Р_n(k-1) + P_n(k) – вероятность наступления события А не более k раз в n испытаниях

- вероятность наступления события А хотя бы один раз в n испытаниях

Р_n(m<k) = 1 - P_n(mk)

P_n(m>k) = 1 - Р_n(m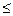k)

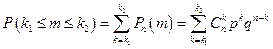- вероятность того, что в n опытах событие А появится от k ₁ до k ₂ раз.

Задача 1. Монету бросают 8 раз. Какова вероятность, что 4 раза выпадет «герб»? Какова вероятность, что более одного раза выпадет «герб»?

р = р(А) = ½, q = р() = ½,

1) n = 8, m = 4, p = q = ½,

P₈(4) =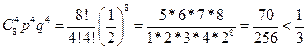

2)

Дата добавления: 2014-01-06