Теорема умножения вероятностей

………………………………………..

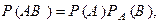
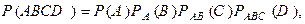Теорема умножения вероятностей для независимых событий. Вероятность произведения двух независимых событий равна произведению их вероятностей, т.е.

.

Аналогичное утверждение справедливо для любого числа независимых событий.

Пример. Два стрелка одновременно выстреливают в мишень. Вероятность попадания для первого стрелка равна 0,6, для второго – 0,8. Найти вероятность того, что в мишени будет:

а) одна пробоина;

б) хотя бы одна пробоина.

Решение. а) Прежде всего, укажем, когда может наступать интересующее нас событие, перебирая все возможные варианты.

В мишени будет одна пробоина

тогда и только тогда, когда

первый стрелок попал и второй стрелок промахнулся

или

первый стрелок промахнулся и второй стрелок попал.

Пусть событие А – в мишени будет одна пробоина, событие 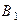– первый стрелок попал, событие – второй стрелок попал. Тогда 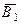– первый стрелок промахнулся,

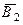– второй стрелок промахнулся. “Тогда и только тогда, когда” соответствует отношению равенства событий. Соединительный союз “или” соответствует операции сложения событий. Соединительный союз “и” соответствует умножению событий. Тогда фраза русского языка, в которой мы перечислили все возможности для наступления события А, равносильна следующему символическому равенству

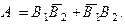
Откуда следует равенство вероятностей

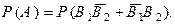
Так как события и несовместны, то, применяя теорему сложения вероятностей для несовместных событий, приходим к равенству

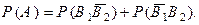
События 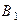,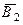и 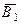,попарно независимы, поэтому, применяя теорему умножения вероятностей для независимых событий, получаем

По условию, и 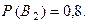Тогда, по свойству взаимно противоположных событий (см. следствие из теоремы сложения вероятностей для несовместных событи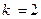й, ), и 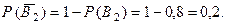Окончательно имеем

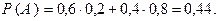
б) Пусть – число попаданий в мишень, тогда искомой является вероятность (заметим, что слова “хотя бы один”, “не менее чем один”, “по-крайней мере один” являются синонимами). Событие равносильно тому, что число попаданий в мишень будет равно 1 или 2, т.е.

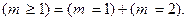
Тогда, учитывая несовместность событи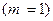й и 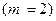, получаем

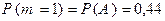(см. п. а) данного примера). Событие 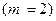(два попадания в мишень) наступает тогда и только тогда, когда первый стрелок попадет в мишень и второй стрелок попадет, т.е.

.

Поэтому

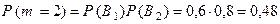
(см. теорему умножения вероятностей для независимых событий). Окончательно имеем

Отметим, что эта задача допускает и другое решение. Так как события и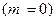взаимно противоположны, то

.

Но Следовательно

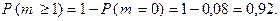
Пример. В коробке лежат4 белых шара и 6 красных. Наудачу, один за другим из коробки извлекается 2 шара. Найти вероятность того, что среди них будет:

а) один красный шар;

б) менее 2-х красных шаров.

Решение. а) Пусть событие А – среди двух извлеченных шаров – ровно один красный. Это событие наступает тогда и только тогда, когда первый из извлеченных шаров – красный, а второй – белый или первый шар – белый, а второй – красный. Напомним, что соединительный союз “или” соответствует сложению событий, союзы “и”, “а” соответствуют умножению событий. Тогда описание всех возможностей наступления события А равносильно следующему формальному равенству

,

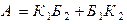где 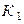(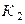) – первый (второй) шар – красный, (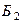) – первый (второй) шар – белый. События и 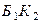– несовместны, поэтому, используя теорему сложения вероятностей для несовместных событий, получаем

.

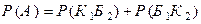Применяя теперь теорему умножения вероятностей, приходим к равенству

.

Для вычисления вероятностей из правой части последнего равенства используем классическое определение вероятности. Тогда

б) Пусть m – число красных шаров среди двух извлеченных. Тогда искомой является вероятность 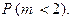Очевидно, что 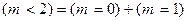, и (см. п. а) данного примера). Вместе с тем, событие 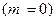– среди извлеченных шаров нет красных – равносильно тому, что первый шар окажется белым и второй – также белым, т.е. , поэтому

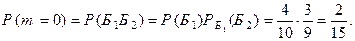
Окончательно имеем

Заметим, что вероятность 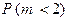может быть также найдена по-другому. События 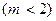и 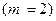взаимно противоположны, поэтому

Но

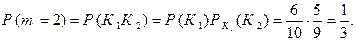
Тогда

Домашнее задание (здесь и далее номера задач указаны по учебнику Н.Ш. Кремера “Теория вероятностей и математическая статистика”): 1.54, 1.58, 1.60, 1.61, 1.64, 1.69.

Дата добавления: 2014-01-06