Нормальный закон распределения. Определение.Непрерывная случайная величина имеет нормальный закон распределенияс параметрами и , если ее плотность распределения имеет вид

Определение. Непрерывная случайная величина имеет нормальный закон распределения с параметрам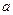и и 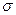, если ее плотность распределения имеет вид

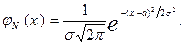
Параметры а и s нормального закона тесно связаны с параметрами распределения рассматриваемой случайной величины. Справедлива следующая теорема.

Теорема. Пусть случайная величина Х имеет нормальный закон распределения с параметрами а и 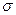. Тогда

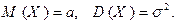
Отметим, что график 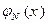– результат деформации Гауссовой кривой 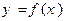(см. § 2.3). Рассмотрим, как изменяется этот график при изменении параметров а и 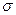нормального закона.

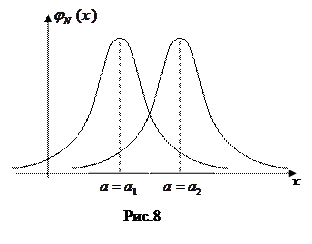
На рис. 8 изображены графики 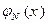при одинаковом значении параметра 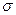: изменение параметра а нормального закона приводит к параллельному переносу графика плотности распределения вдоль оси абсцисс.

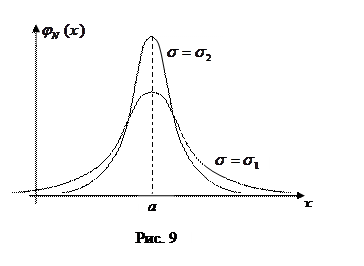
На рис. 9 изображены графики 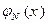при одинаковом значении параметра а: изменение параметра 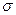нормального закона приводит к “растяжению” графика вдоль оси ординат при сохранении площади под кривой равной 1 (заметим, что на рис. 9 ).

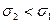Теорема. Пусть случайная величина Х имеет нормальный закон распределения с параметрами а и 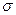. Тогда справедливы формулы:

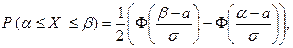(1)

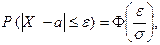(2)

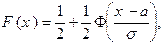
где 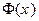– функция Лапласа, – функция распределения случайной величины Х.

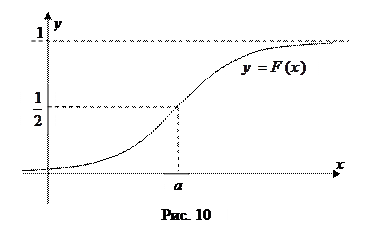
Заметим, что график функции распределения нормально распределенной случайной величины получается в результате деформации из графика функции Лапласа (см. рис. 10 и 2).

Пример. Случайная величина Х – ошибка измерительного прибора распределена по нормальному закону с дисперсией равной 16 мк².

Систематическая ошибка отсутствует. Найти вероятность того, что при одном измерении ошибка:

а) превзойдет по модулю 6 мк;

б) окажется в промежутке от 0,5 до 3,5 мк.

Решение. а) Отсутствие систематической ошибки означает, что значения случайной величины Х группируются около нуля, поэтому 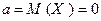(см. § 3.3). Искомой является вероятность 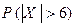. Воспользуемся переходом к противоположному событию: 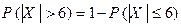. Так как ,

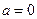то 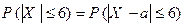, т.е. последняя вероятность точно того вида, что может быть вычислена по формуле (2). Используя формулу (2) при 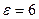, , 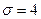получаем

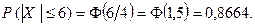
Окончательно имеем

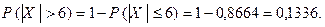
б) Искомая вероятность вычисляется по формуле (1) при :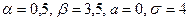

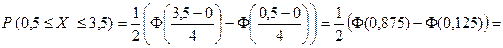
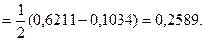
Упражнение. Пусть случайная величина Х нормально распределена с параметрами а и s. Проверить, что 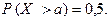Дать геометрическую интерпретацию этому результату.

Домашнее задание. 3.62, 3.63, 3.65, 3.66.

Дата добавления: 2014-01-06