Теоремы Бернулли и Чебышёва

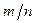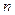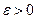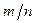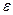Теорема Бернулли. Пусть – частость наступления события А в повторных независимых испытаниях, в каждом из которых это событие наступает с вероятностью .Тогда для произвольного вероятность того, что частость будет отличаться от вероятности не более чем на (по абсолютной величине) неограниченно приближается к 1 при неограниченном увеличении значения 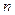, т.е.

Другими словами, теорема Бернулли утверждает, что частость 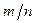наступления некоторого события сходится по вероятности к вероятности наступления этого события.

Доказательство. Учитывая, что вероятность произвольного события не превосходит 1, из неравенства Бернулли следует

Переходя к пределу при 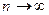, получаем

Крайние левый и правый пределы этого двойного неравенства равны 1. Таким образом, имеем

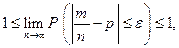
что равносильно утверждению теоремы Бернулли.

Теорема Бернулли утверждает, что, если за значение вероятности некоторого события взять значение частости 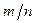наступления этого события, найденную по результатам 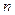испытаний, то вероятность погрешности (даже сколь угодно малой) приближенного равенства будет стремиться к нулю с увеличением числа испытаний .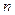

Теорема Чебышёва. Пусть случайные величины 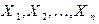независимы, одинаково распределены и Тогда для произвольного 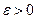вероятность того, что среднее арифметическое этих случайных величин отличается от их общего математического ожидания не более чем на 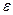(по абсолютной величине), неограниченно приближается к 1 при неограниченном увеличении числа 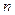этих случайных величин т.е.

Другими словами, теорема Чебышёва утверждает, что среднее арифметическое некоторого числа случайных величин, имеющих одинаковое математическое ожидание, сходится по вероятности к их общему математическому ожиданию.

Говоря о приложениях теоремы Чебышёва, отметим, в первую очередь, следующую возможность. Если за значение некоторого неизвестного параметра а взять среднее арифметическое результатов 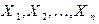независимых измерений этого параметра, то вероятность погрешности (даже сколь угодно малой) приближенного равенства будет стремиться к нулю при неограниченном увеличении числа 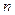этих измерений.

Теоремы Бернулли и Чебышёва являются явными реализациями так называемого закона больших чисел, утверждающего, что при проведении достаточно большого числа испытаний погрешности отдельных испытаний взаимно погашают друг друга (тем самым среднее арифметическое независимых случайных величин – результатов этих испытаний – стремится к постоянной величине при неограниченном увеличении числа испытаний).

Домашнее задание:6.10, 6.11, 6.17, 6.19, 6.22.

Дата добавления: 2014-01-06