
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Первичная обработка результатов эксперимента. Характеристики вариационных рядов
|
|
|
|
Пусть произведено 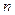 независимых измерений некоторой случайной величины
независимых измерений некоторой случайной величины 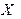 :
:  – результат первого измерения,
– результат первого измерения, 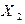 – результат второго измерения, …,
– результат второго измерения, …,  – результат
– результат 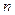 -го измерения. Тогда через
-го измерения. Тогда через 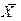 обозначим среднее арифметическое результатов
обозначим среднее арифметическое результатов 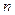 измерений рассматриваемой случайной величины
измерений рассматриваемой случайной величины 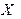 , то есть
, то есть
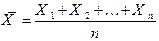 .
.
Заметим, что, поскольку 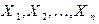 – случайные величины, то
– случайные величины, то 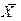 также является случайной величиной.
также является случайной величиной.
Пример. Детали некоторого вида расфасованы по ящикам. Результаты обследования шести из этих ящиков (на предмет наличия в них бракованных деталей) представлены в таблице:

| ||||||

|
где 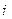 – номер ящика,
– номер ящика,  – число бракованных деталей в
– число бракованных деталей в  -ом ящике.
-ом ящике.
Тогда

Приведенное вычисление подсказывает возможность более компактного представления результатов обследования, а именно – использование таблицы следующего вида:
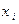
| 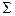
| |||
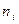
|
где 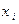 – число бракованных деталей в ящике;
– число бракованных деталей в ящике; 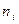 – число ящиков.
– число ящиков.
Такая таблица называется вариационным рядом. Аналогично, в общем случае имеем
Определение. Вариационным рядом признака 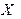 называется таблица вида
называется таблица вида
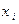
| 
| 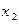
| … | 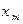
| 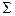
|
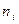
| 
| 
| … | 
| 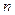
|
где 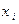 – возможные значения данного признака,
– возможные значения данного признака, 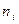 – числа объектов,
– числа объектов, 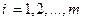 ,
, 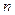 – число обследованных объектов (
– число обследованных объектов ( ).
).
Отметим, что величины 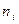 , значения которых заполняют нижнюю строку вариационного ряда, называются эмпирическими частотами.
, значения которых заполняют нижнюю строку вариационного ряда, называются эмпирическими частотами.
Очевидно, что признак 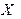 , для которого строится вариационный ряд, есть случайная величина.
, для которого строится вариационный ряд, есть случайная величина.
В том случае, когда результаты обследования представлены вариационным рядом, формула для вычисления 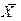 имеет вид
имеет вид
 (1)
(1)
Сама величина 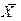 в этом случае называется средней вариационного ряда или выборочной средней. Появление в данном случае дополнительного эпитета выборочный связано с тем, что обследованные объекты выбираются из некоторой объемлющей (так называемой генеральной) совокупности объектов.
в этом случае называется средней вариационного ряда или выборочной средней. Появление в данном случае дополнительного эпитета выборочный связано с тем, что обследованные объекты выбираются из некоторой объемлющей (так называемой генеральной) совокупности объектов.
|
|
|
Напомним, что 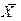 есть случайная величина. В тех случаях, когда данные эксперимента представлены вариационным рядом, а
есть случайная величина. В тех случаях, когда данные эксперимента представлены вариационным рядом, а 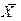 вычисляется по формуле (1), случайными являются эмпирические частоты
вычисляется по формуле (1), случайными являются эмпирические частоты 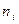 .
.
Вариационный ряд является оценкой закона распределения случайной величины (признака) 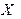 . Поясним, почему это так. По вариационному ряду построим равнозначную ему таблицу, заменяя строку эмпирических частот
. Поясним, почему это так. По вариационному ряду построим равнозначную ему таблицу, заменяя строку эмпирических частот 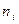 частостями
частостями 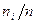 . В результате имеем:
. В результате имеем:
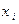
| 
| 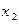
| … | 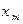
| 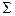
|

| 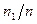
| 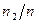
| … | 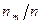
|
Учитывая, что частости  являются оценками вероятностей
являются оценками вероятностей 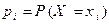 (
(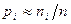 , см. § 7.1), приходим к требуемому утверждению.
, см. § 7.1), приходим к требуемому утверждению.
Принимая во внимание последнее замечание, получаем
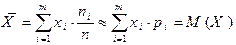 .
.
Таким образом, средняя вариационного ряда (выборочная средняя) 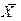 является оценкой математического ожидания
является оценкой математического ожидания 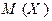 той случайной величины (признака)
той случайной величины (признака) 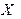 , для которой построен данный вариационный ряд. Можно доказать, что эта оценка является несмещенной и состоятельной.
, для которой построен данный вариационный ряд. Можно доказать, что эта оценка является несмещенной и состоятельной.
Учитывая полученные результаты, аналогично построим оценку для дисперсии 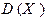 случайной величины
случайной величины 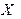 :
:
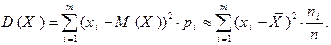
Выражение, стоящее в правой части последнего равенства называется выборочной дисперсией и обозначается 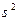 , то есть
, то есть
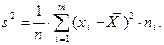
Выборочная дисперсия 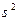 – оценка для дисперсии
– оценка для дисперсии 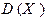 случайной величины
случайной величины 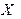 . Можно доказать, что выборочная дисперсия
. Можно доказать, что выборочная дисперсия 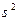 является смещенной оценкой для
является смещенной оценкой для 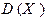 , то есть
, то есть 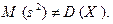 Несмещенная оценка
Несмещенная оценка  для
для  определяется равенством
определяется равенством

Заметим, что для вычисления выборочной дисперсии удобно использовать формулу – аналог свойства 3 дисперсии (см. § 3.3):

Определение. Вариационный ряд называется дискретным, если число возможных значений признака– конечно, и непрерывным (интервальным), если возможные значения признака полностью заполняют некоторый интервал.
Вариационные ряды, которые встречались нам до сих пор в данном параграфе, являются дискретными. Рассмотрим пример интервального вариационного ряда.
|
|
|
Пример. По результатам обследования некоторого малого предприятия получены следующие данные о ежемесячной заработной плате его сотрудников:
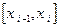
| 5 – 15 | 15 – 25 | 25 – 35 | 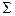
|
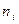
|
где 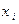 – размер заработной платы (ден. ед.),
– размер заработной платы (ден. ед.), 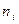 – число сотрудников.
– число сотрудников.
Для нахождения параметров непрерывного вариационного ряда – выборочной средней, выборочной дисперсии – этот вариационный ряд сначала сводится к дискретному (в результате выбора середины для каждого из рассматриваемых интервалов), после чего 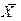 и
и 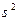 вычисляются по приведенным выше формулам.
вычисляются по приведенным выше формулам.
Например, данный интервальный вариационный ряд сводится к следующему дискретному:
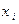
| 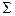
| |||
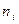
|
Тогда

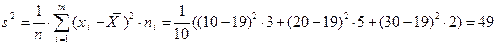
или

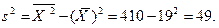
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 270; Нарушение авторских прав?; Мы поможем в написании вашей работы!