
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема о минимаксе
|
|
|
|
Возможность нахождения каждым игроком своей наилучшей стратегии основывается на следующей теореме, которая может рассматриваться как доказательство существования решения для конечных игр.
Теорема. Всякая конечная антагонистическая игра имеет цену, и у каждого игрока существует по меньшей мере одна оптимальная стратегия.
Исходные предпосылки. Пусть  — конечная игра, а
— конечная игра, а 
 — смешанное расширение этой игры. При доказательстве теоремы удобно вести рассуждения в терминах S-игры, поэтому через
— смешанное расширение этой игры. При доказательстве теоремы удобно вести рассуждения в терминах S-игры, поэтому через 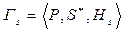 обозначим эквивалентную S-игру.
обозначим эквивалентную S-игру.
Нижняя и верхняя цены S-игры будут равны  и
и  соответственно, независимо от того, рассматривают игру G или эквивалентную ей S-игру
соответственно, независимо от того, рассматривают игру G или эквивалентную ей S-игру 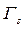 , причем
, причем  .
.
Для того, чтобы доказать теорему, достаточно показать, что 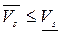 , так как из сравнения с предыдущим неравенством будет следовать
, так как из сравнения с предыдущим неравенством будет следовать  , т.е. что игра имеет цену.
, т.е. что игра имеет цену.
Для доказательства этого неравенства достаточно найти такую смешанную стратегию 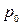 первого игрока, при которой для всех
первого игрока, при которой для всех 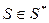 имеет место
имеет место
 . (1)
. (1)
Действительно, если неравенство (1) имеет место, то
 . Таким образом, доказательство теоремы будет сводиться к доказательству неравенства (1).
. Таким образом, доказательство теоремы будет сводиться к доказательству неравенства (1).
Доказательство. Рассмотрим множество T, состоящее из точек  таких, что
таких, что  . На рисунке показана область T для двумерного пространства, которая в данном случае имеет вид прямоугольного клина с вершиной, лежащей на прямой, проведенной из начала координат под углом
. На рисунке показана область T для двумерного пространства, которая в данном случае имеет вид прямоугольного клина с вершиной, лежащей на прямой, проведенной из начала координат под углом 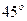 к оси абсцисс. Рассмотрим некоторые свойства множества T.
к оси абсцисс. Рассмотрим некоторые свойства множества T.

Множество T является выпуклым. Рассмотрим произвольные точки 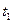 и
и  этого множества. Уравнение отрезка, соединяющего эти две точки, будет иметь вид:
этого множества. Уравнение отрезка, соединяющего эти две точки, будет иметь вид:
 ,
,  ,
,  .
.
Проектируя это уравнение на i-ую ось и учитывая теорему на стр.14, получаем
 (2) Следовательно, любая точка рассматриваемого отрезка принадлежит T и множество T выпуклое.
(2) Следовательно, любая точка рассматриваемого отрезка принадлежит T и множество T выпуклое.
Множество T не пересекается с множеством 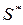 . Это следует из того, что любая точка множества
. Это следует из того, что любая точка множества 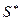 имеет по крайней мере одну координату, большую или равную
имеет по крайней мере одну координату, большую или равную  (следствие 1 из теоремы «Если S — произвольная точка m-мерного пространства и
(следствие 1 из теоремы «Если S — произвольная точка m-мерного пространства и 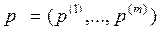 — многомерная переменная, то имеет место соотношение
— многомерная переменная, то имеет место соотношение  , а значит T и
, а значит T и 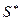 не имеют общих точек.
не имеют общих точек.
Поскольку T и 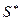 — выпуклые непересекающиеся области, то существует разделяющая их гиперплоскость такая, что множества T и
— выпуклые непересекающиеся области, то существует разделяющая их гиперплоскость такая, что множества T и 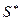 окажутся в разных полупространствах, определяемых этой гиперплоскостью. Следовательно, существует такое
окажутся в разных полупространствах, определяемых этой гиперплоскостью. Следовательно, существует такое 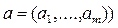 и число c, что уравнение
и число c, что уравнение
 (3)
(3)
будет уравнением разделяющей гиперплоскости, причем
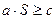 для
для  ;
;
 для
для  . (4)
. (4)
Покажем, что 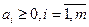 . Пусть
. Пусть  — точка, у которой i-ая координата равна 1, а остальные равны малой величине
— точка, у которой i-ая координата равна 1, а остальные равны малой величине 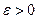 . Рассмотрим точку
. Рассмотрим точку  . Так как ее максимальная координата равна
. Так как ее максимальная координата равна  (следствие 2 из теоремы «Если S — произвольная точка m-мерного пространства и
(следствие 2 из теоремы «Если S — произвольная точка m-мерного пространства и  — многомерная переменная, то имеет место соотношение
— многомерная переменная, то имеет место соотношение  , то точка
, то точка  . Следовательно,
. Следовательно,
 .
.
Отсюда следует, что
 .
.
Если  , то
, то 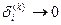 при
при  и
и 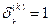 при этом последнее условие дает
при этом последнее условие дает
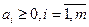 . (5)
. (5)
Введем обозначение
 . (6)
. (6)
Очевидно, что 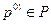 , так как
, так как
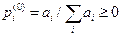 ,
, 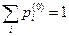 .
.
Кроме того, введем обозначение  . (7)
. (7)
Поделим неравенства (4) на 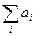 . С учетом (6) и (7) получим
. С учетом (6) и (7) получим
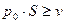 для
для  ;
;
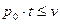 для
для  . (8)
. (8)
Рассмотрим точку  с координатами
с координатами 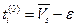 ,
, 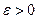 ,
, 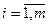 . Очевидно, что
. Очевидно, что 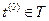 . На основании второго неравенства из (8) получаем
. На основании второго неравенства из (8) получаем
 . (9)
. (9)
Пусть  , так что
, так что  . Тогда
. Тогда
 . (10)
. (10)
Сравнивая (9) и (10), находим  (11)
(11)
При этом первое из неравенств (8) дает  , (12), что и доказывает неравенство (1).
, (12), что и доказывает неравенство (1).
Таким образом,  является ценой игры, а
является ценой игры, а 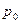 и
и 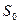 представляют собой оптимальные смешанные стратегии игроков. Теорема доказана.
представляют собой оптимальные смешанные стратегии игроков. Теорема доказана.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 678; Нарушение авторских прав?; Мы поможем в написании вашей работы!