Доминирующие и полезные стратегии

Решение антагонистических игр.

Для упрощения исследования игр стараются исключить из анализа игры те стратегии, которые при разумном подходе вряд ли могут быть использованы в какой-либо из партий игры. Те стратегии игроков, которые используются или могут быть использованы в какой-либо из партий игры, называются рабочими.

Упрощение заключается в выявлении рабочих стратегий из всех возможных. Так как нас интересуют смешанные стратегии, то рабочие стратегии выбираются с вероятностью, отличной от 0, а не рабочие с вероятностью 0. Для выявления рабочих стратегий используется отношение доминирования (преобладания).

Рассмотрим два вектора стратегий второго игрока: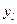и . Величина проигрыша второго игрока определяется соответственно 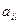и 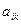, 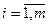. Возможны следующие ситуации:

1) Если 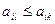и среди 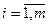найдется такое j, что 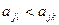, т.е. в матрице игры потери в столбце l не превосходят соответствующих потерь в столбце k, то говорят, что стратегия 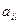доминирует над стратегией 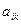, т.е. получаем доминирование по столбцам . В этом случае стратегия должна быть отброшена, т.е. вычеркнута из матрицы игры;

2) Если же 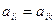, , то эти стратегии дублируют друг друга.

В любом из этих случаев стратегию можно удалять из матрицы без изменения оптимальной стратегии второго игрока.

Доминирующие стратегии второго игрока имеют наглядную геометрическую иллюстрацию при переходе к эквивалентной S-игре на плоскости. В этом случае 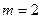и

, .

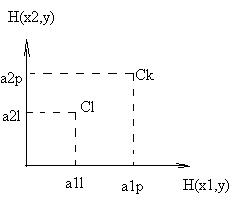На рисунке приведены два случая расположения точек 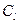и , соответствующие чистым стратегиям 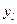и второго игрока. Легко видеть, что на рисунке (а) стратегия 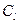доминирует над стратегией , а на рисунке (б) ни одна из стратегий не является доминирующей. Для того, чтобы стратегия 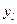доминировала над стратегией , точка 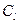должна лежать левее и ниже точки .

(а) (б)

Аналогичным образом определяют доминирующие стратегии первого игрока. Стратегия доминирует над стратегией , если выигрыш первого игрока при стратегии больше выигрышей при стратегии при любой стратегии y:

,

т.е. если в матрице игры выигрыши в строке больше соответствующих выигрышей строки .

Пример. Предположим, что есть игра

.

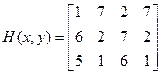Воспользуемся отношением доминирования для упрощения игры:

1) 2 и 4 столбцы одинаковые, поэтому получаем игру ;

2) Сравниваем 2 и 3 строки. Элементы во второй строке превосходят элементы в первой, поэтому первый игрок никогда не будет выбирать 3 стратегию, т.к. вторая принесет ему большую прибыль, значит получаем игру ;

3) Сравниваем 1 и 3 столбец, 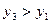, значит получаем игру :

.

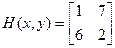Таким образом, отношение доминирования по строкам заключается в том, что все , 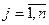и есть r такое, что , то .

Дата добавления: 2014-01-06