
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Смешанное расширение бескоалиционной игры
|
|
|
|
Рассмотрим бескоалиционную игру двух лиц Г=<X1,X2,H1,H2>. В простейшем случае X1={x1(1),x2(1)}; X2={x1(2),x2(2)}. Тогда
для 1-ого игрока x1(1) 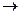 p (p — вероятность выбора стратегии x1(1)), x2(1)
p (p — вероятность выбора стратегии x1(1)), x2(1) 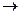 1-p
1-p
для 2-ого игрока x1(2) 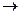 q (q — вероятность выбора стратегии x1(2)), x2(2)
q (q — вероятность выбора стратегии x1(2)), x2(2) 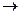 1-q
1-q
В общем случае, если число стратегий m и n, получим
xi(1) 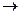 pi,
pi, 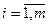 ,
, 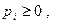
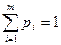
xj(2) 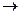 qj,
qj, 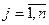 ,
, 
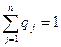
Важнейшим принципом смешанного решения бескоалиционной игры является то, что игроки выбирают свои стратегии независимо. Тогда для каждой ситуации x(i)= вероятность ее появления будет равна P(x(i))=pi*qj
вероятность ее появления будет равна P(x(i))=pi*qj
Аналогично это понятие можно обобщить на случай N игроков. В этом случае множество всех ситуаций Х будет определяться так:
I={1,…,N} X=X1*X2*…*XN
Каждая ситуация х Х будет иметь вероятность P(x)=p(x(1))* p(x(2))*… p(x(N)), где х — ситуация выбора игроками стратегии х=(x(1), x(2),…, x(N)), причем
Х будет иметь вероятность P(x)=p(x(1))* p(x(2))*… p(x(N)), где х — ситуация выбора игроками стратегии х=(x(1), x(2),…, x(N)), причем 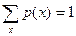
Для биматричных игр доказывается, что существует ситуация (p*,q*), которая является ситуацией равновесия по Нэшу.
ДОК-ВО (Петросян с.130)
Рассмотрим свойства равновесия по Нэшу на примере анализа биматричной игры 2*2.
X1={ x1(1), x2(1)} A/B=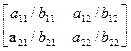
X2={ x1(2), x2(2)}
Вероятности выбора стратегий: x1(1) 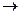 p x1(2)
p x1(2) 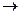 q
q
x2(1) 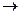 1-p x2(2)
1-p x2(2) 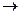 1-q
1-q
Найдем выигрыш Н1 в ситуации (p,q)
H1(p,q)=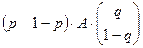
H2(p,q)=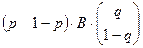
Найдем p и q, которые обеспечат ситуацию равновесия по Нэшу:
H1(p,q)=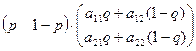 =
=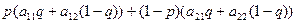 =
=
=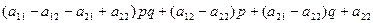 =
=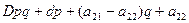
H2(p,q)=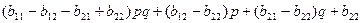 =
=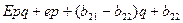
Ситуация для 1-ого игрока, когда р (0,1) будет предпочтительней, если будут выполняться 2 неравенства:
(0,1) будет предпочтительней, если будут выполняться 2 неравенства:
H1(1,q) 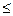 H1(p,q)
H1(p,q)
H1(0,q) 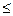 H1(p,q)
H1(p,q)
Обозначим 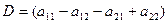
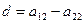
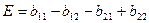
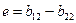
Тогда из первого неравенства получаем:
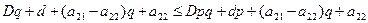
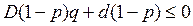
из второго неравенства:
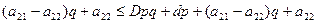
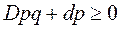
если выполняются эти два неравенства, то ситуация предпочтительна для 1-ого игрока
Аналогично получаем условия предпочтительности ситуации (p,q) при 0<q<1 для 2-го игрока:
H2(p,1) 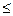 H2(p,q)
H2(p,q)
H2(p,0) 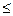 H2(p,q)
H2(p,q)
Первое неравенство:
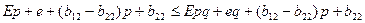
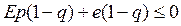
Второе неравенство:
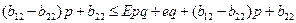
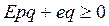
Таким образом, эти 4 неравенства определяют предпочтительность ситуации (p,q). Доказано, что эти неравенства совместны тогда и только тогда, когда они обращаются в равенства. В этом случае имеем следующее решение:
p*= 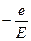 ; q*=
; q*= 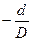
или p*= 
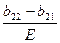 ; q*=
; q*=
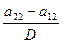
Получается, что стратегии игроков зависят от стратегий противников.
Рассмотрим матричную игру с матрицей A=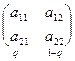 , тогда
, тогда
a11q + a12(1-q) = a21q + a22(1-q), откуда  q*=
q*=
ПРИМЕР. A=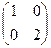 B=
B=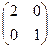
p*=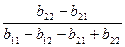 =
=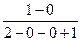 =
=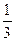 — вероятность выбора 1-ым игроком стратегии х1
— вероятность выбора 1-ым игроком стратегии х1
q*=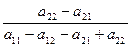 =
=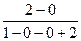 =
=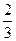 — вероятность выбора 2-ым игроком своей стратегии у1
— вероятность выбора 2-ым игроком своей стратегии у1
Вывод: нет решения, удовлетворяющего обоих игроков. В этом случае необходимо договариваться.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 333; Нарушение авторских прав?; Мы поможем в написании вашей работы!