
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пространство стратегий статистика и функция выигрыша
|
|
|
|
X — множество стратегий статистика, аналогичное множеству стратегий в антагонистических играх. Если множество X — дискретное, X = (x ,…, x
,…, x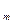 ), тогда можно рассматривать множество ситуаций и множество выигрышей статистика в этих ситуациях: (x
), тогда можно рассматривать множество ситуаций и множество выигрышей статистика в этих ситуациях: (x , z
, z ), i =
), i =  , j =
, j = 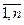
П = (a ) m*n
) m*n
Эта функция П называется функцией потерь. Значение функции потерь позволяет игроку 1 (статистику) принимать предпринимать правильные действия.
Пример: Задача о яйцах и креме
| Состояние яйца | ||
| Действие | Z1 - хорошее | Z2- испорченное |
| долить в остальные 5 яиц, x1 | крем из 6 яиц | крема нет, загублено 5 хороших яиц |
| вылить разбитое яйцо на блюдце для контроля, x2 | крем из 6 яиц, но надо мыть посуду (блюдце) | крем из 5 яиц, надо мыть блюдце "с отвращением" |
| выбросить яйцо, не глядя, x3 | крем из пяти яиц, загублено 1 яйцо | крем из 5 яиц |
Если каким-либо образом оцифровать описание ситуации в виде значений функций потерь, то получим игру с природой.
В описании игры с природой наблюдается полная аналогия с антагонистической игрой. Статистик может принимать чистые стратегии x
 X и их вероятностные оценки p
X и их вероятностные оценки p = p(x
= p(x )
) P, (X, P) — пространство стратегий статистика.
P, (X, P) — пространство стратегий статистика.
А = (a ), i =
), i =  ; j =
; j = 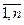
X = 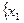 ,…,
,…, , m — чистые стратегии статистика;
, m — чистые стратегии статистика;
n — чистые состояния природы;
Z = 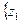 ,…,
,…,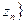
Если используются смешанные стратегии, то каждому из состояний чистой стратегии сопоставляется значение p , i =
, i =  . Определим вероятность использования смешанных стратегий.
. Определим вероятность использования смешанных стратегий.
x~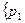 ,…,
,…, 
z~ ,…,
,…, 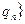 — вероятность состояний природы.
— вероятность состояний природы.
Если эти вероятности известны, то можно определить сравнительные вероятности статистика в этой игре:
M[S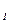 , S
, S ] =
] = 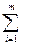
 a
a *p
*p *q
*q
S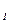 — множество (X*P)
— множество (X*P)
S — множество (Z*Q)
— множество (Z*Q)
p = 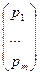 ; q =
; q = 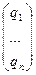
M[S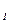 , S
, S ] = p
] = p *A*q
*A*q
Задачу статистика в этой игре можно определить как нахождение такого S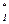 , при котором его выигрыш M[S
, при котором его выигрыш M[S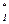 , S
, S ]
] 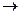 max. Эта стратегия S
max. Эта стратегия S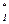 может быть как чистой, так и смешанной.
может быть как чистой, так и смешанной.
Исходя из этого, в матрице платежей (a ) можно рассматривать доминирующие и доминируемые стратегии.
) можно рассматривать доминирующие и доминируемые стратегии.
Доминирование по строкам и доминирование по столбцам теряет смысл, т. к. природа не выиграет и не проиграет, ей безразлично её состояние.
С учётом этого матрица платежей не в полной мере характеризует достоинства и недостатки каждой стратегии X = 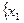 ,…,
,…, игрока.
игрока.
Используют другую форму описания игры, которая более полно отражает степень удачливости в выборе игрока. Одним из таких показателей является матрица рисков:
A = 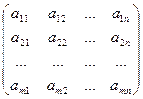
Номер столбца матрицы совпадает с состоянием природы, номер строки характеризует стратегию игрока. B = max a
= max a — максимальный выигрыш статистика при данном состоянии природы j.
— максимальный выигрыш статистика при данном состоянии природы j.
R = (r ), i =
), i =  , j =
, j = 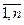
r = B
= B - a
- a — разница между максимальным выигрышем и выигрышем, который получит статистик, выбирая стратегию x
— разница между максимальным выигрышем и выигрышем, который получит статистик, выбирая стратегию x .
.
Матрица рисков: R =  . В матрице рисков хотя бы один из элементов в каждом столбце должен равняться нулю.
. В матрице рисков хотя бы один из элементов в каждом столбце должен равняться нулю.
Пример: А = 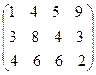 ; R =
; R = 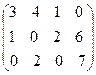
Если условием выбора стратегии является максимум среднего выигрыша, то по матрице рисков R min. Если же вероятности состояния природы известны (q
min. Если же вероятности состояния природы известны (q ), то условие максимума среднего выигрыша и условие минимума среднего риска дают одни и те же стратегии.
), то условие максимума среднего выигрыша и условие минимума среднего риска дают одни и те же стратегии.
Если V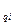 =
=  ; V
; V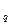 = max
= max V
V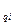 или r
или r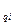 =
=  ; r
; r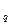 =min
=min r
r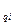 , то решение будут одинаковыми.
, то решение будут одинаковыми.
Пример: Матрица платежей: А = 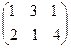 ; q = (0,2; 0,5; 0,3)
; q = (0,2; 0,5; 0,3)
V = 1*0,2+ 3*0,5+ 1*0,3 = 2
= 1*0,2+ 3*0,5+ 1*0,3 = 2
V = 2*0,2+ 0,5+ 1,2 = 2,1
= 2*0,2+ 0,5+ 1,2 = 2,1
V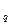 = 2,1; x
= 2,1; x является предпочтительной стратегией: x
является предпочтительной стратегией: x даёт больший средний выигрыш V
даёт больший средний выигрыш V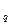 .
.
R = 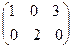 r
r = 0,2+ 0,9 = 1,1
= 0,2+ 0,9 = 1,1
r = 1
= 1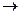 x
x — риск минимален.
— риск минимален.
О вероятностях состояния природы в лучшем случае известны их некоторые оценки q’. На практике достоверность этих оценок является слишком низкой для того, чтобы использовать их при оценке качества выбора решений статистика.
В таких условиях лучше:
1. Не пользоваться этими оценками и для выбора решения использовать критерий, который не пользуется понятием вероятности состояния природы;
2. Cчитать все состояния природы равновероятными q = 1/n, i=
= 1/n, i=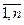 .
.
Критерий, позволяющий принять задачу выбора решения, называется критерием выбора решений при неопределённости.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 461; Нарушение авторских прав?; Мы поможем в написании вашей работы!