Теория растворов сильных электролитов Дебая и Хюккеля

Сильные электролиты в растворе находятся практически только в виде ионов

K_mA_n → Kⁿ⁺ + A^m-

Однако, найденные опытным путем значения электрической проводимости, изотонического коэффициента, степени диссоциации и других показателей для сильных электролитов оказываются меньше, чем можно было бы ожидать при 100%-ной диссоциации.

Например: для K₂SO₄ теоретическое значение i=3. Экспериментальное значение i (определенное по понижению температуры замерзания) = 2,46. Экспериментальное значение степени диссоциации 73%.

С другой стороны полная диссоциация сильных электролитов на ионы подтверждается физическими и физико-химическими методами. Например, значения теплоты нейтрализации всех сильных кислот сильными основаниями практически одинаковы ΔH = -56,5 кДж/моль, что свидетельствует о полной диссоциации разбавленных растворов кислот и оснований.

Кроме того, исследование концентрированных растворов сильных электролитов оптическими методами показало отсутствие молекул в их растворах.

Приведенное противоречие объясняется в теории Дебая и Хюккеля электростатическим межионным взаимодействием в растворах.

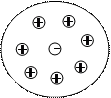В водных растворах сильные электролиты практически полностью диссоциированы, в растворе содержится большое количество ионов, расстояние между которыми мало. В результате около каждого иона находятся преимущественно ионы противоположного знака, и образуется так называемая “ионная атмосфера”.

Как следствие, возникает эффект уменьшения числа ионов, участвующих в химических процессах. Ионы ориентируются друг относительно друга и поэтому их эффективная концентрация (активность) отличается от истинной.

Под активностью электролита x понимают эффективную концентрацию в соответствии с которой он участвует в различных процессах.

Активность связана с истинной концентрацией растворенного вещества

a(x) = f(x)∙C(x)

a(x) – активность электролита, моль/л

C(x) – концентрация, моль/л

f(x) – коэффициент активности (величина безразмерная)

Коэффициент активности 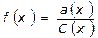выражает отклонение раствора с концентрацией C(x) от поведения раствора при бесконечном разведении, т.е. в отсутствии межионных взаимодействий.

Если f(x) = 1 – это означает, что движения ионов не ограничены действием электростатических сил и a=C.

Если f(x) < 1, то на движение ионов оказывает влияние их электростатическое взаимодействие и вместо концентрации C надо подставлять активность a.

Если f(x) = 1 → a(x) = C(x)

Если f(x) < 1 → a(x) < C(x)

Активность (эффективная концентрация) ионов какого-то одного вида из-за их взаимодействия зависит от общего содержания ионов в растворе. Мерой этого общего содержания ионов является ионная сила раствора I

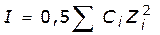
I – это полусумма произведений концентраций ионов на квадрат их зарядов. Для устранения влияния знака заряда необходимо возведение Z (заряда) в квадрат. Из определения следует, что ионная сила должна измеряться в тех же единицах, что и концентрация. (На практике часто ее пишут без размерности).

Ионная сила бинарного электролита, диссоциирующего на 2 однозарядных иона численно равна его концентрации.

[I] = [C] = [моль/л]

Например: AB (KCl → K⁺ + Cl^-)

I = 0,5(0,1∙1² + 0,1∙1²) = 0,1

Во сколько раз ионная сила больше концентрации для электролита типа A₂B₃, например для

Al₂(SO₄)₃

Пусть концентрация данного электролита условно равна C

[Al⁺³] = 2C

[SO₄^2-] = 3С

I = 0,5(2C∙3² + 3C∙2²) = 15C, J = 15 С, т.е. в 15 раз

Еще рассмотрим пример: фосфатный буфер

Пусть C₁ = C(NaH₂PO₄) = 0,1M

C₂ = C(Na₂ HPO₄) = 0,05M

Находим концентрации ионов:

[Na⁺] = C₁ + 2C₂ = 0,1 + 2∙0,05 = 0,2M

[H₂PO₄^-] = 0,1

[HPO₄^2-] = 0,05

I = 0,5(0,2∙1² + 0,1∙1² + 0,05∙2²) = 0,25

Рассмотрим на примере 0,01M раствора алюмокалиевых квасцов K₂SO₄∙Al₂(SO₄)₃∙2H₂O

[K⁺] = 0,01∙2 = 0,02

[SO₄^2-] = 0,01∙4 = 0,04

[Al³⁺] = 0,01∙2 = 0,02

I = 0,5(0,02∙1² + 0,04∙2² + 0,02∙3²) = 0,18

В 1923 Дебай и Хюккель показали, что для разбавленных водных растворов с ионной силой I ≤ 0,01 коэффициенты активности ионов можно рассчитать по формуле

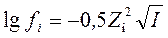
f_i – коэффициент активности i-го катиона (аниона)

Z_i – заряд i-го катиона (аниона)

Данное уравнение является математическим выражением предельного закона Дебая–Хюккеля (1921): в разбавленных растворах сильных электролитов с одинаковой ионной силой коэффициенты активности катионов и анионов одинаковой зарядности равны независимо от их химической природы.

Приведенная формула справедлива лишь для растворов с низкой ионной силой I ≤ 0,01, потому-то и выражает предельный закон.

Электрохимия - это раздел химии, который изучает закономерно­сти химических реакций при действии электрического поля на вещество и, наоборот, электрические явления при химических реакциях. В первом случае электрическая энергия превращается в химическую, а во втором -химическая энергия переходит в электрическую. Введем некоторые понятия.

1) Проводники 1 рода - это металлы и сплавы, в них ток переносится электронами.

Для проводников I рода, как известно, сопротивление подсчитыва­ется по формуле

(1) 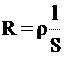ρ - удельное сопротивление,

l - длина проводника,

S - площадь поперечного сечения.

2) Проводники II рода - это растворы и расплавы электролитов, в них ток переносится ионами.

Способность проводить электрический ток у растворов электроли­тов неодинакова и зависит от многих факторов, в частности от количест­ва ионов и скорости их движения.

Чем больше концентрация ионов, тем сильнее электростатическое взаимодействие ионов, которое снижает их скорость.

При разбавлении водой сильных электролитов концентрация ио­нов, а следовательно, межионное взаимодействие, и тормозящие эффек­ты уменьшаются, поэтому растет скорость движения ионов,

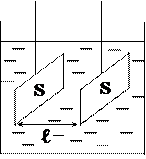В растворах слабых электролитов концентрация ионов невелика, и поэтому их скорость движения практически не зависит от разбавления. Сопротивление растворов измеряют с помощью кондуктометрической ячейки.

3) Кондуктометрическая ячейка- это сосуд

с двумя металлическими электродами площадью S,

находящихся на расстоянии l друг от друга (учебник

Ершова, стр. 452). С помощью кондуктометрической

ячейки измеряется сопротивление растворов.

Для электролитов используют понятие удельная электрическая проводимость. Эта величина обозначается буквой (каппа).

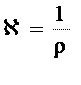(2)

Численно удельная электрическая проводимость равна электро­проводности раствора, находящегося между двумя электродами площа­дью 1м² и отстоящими друг от друга на 1 м, т.е. это электропровод­ность 1 м³ раствора.

Из уравнений (1) и (2) следует

Зависимость удельной электрической проводимости от разбав­ления представлена на следующем рисунке (учебник Ершова, стр. 454).

1 - слабый электролит,

2 - сильный электролит,

C - молярная концентрация вещества,

V - разбавление раствора, V=1/C

Исходное значение сильных электролитов больше, чем слабых, т.к. у слабых элек­тролитов низкая концентрация ионов. Вначале при разбавлении растет, несмотря на уменьшение кон­центрации вещества в растворе. Для слабых электролитов это объясняет­ся тем, что при разбавлении увеличивается α - степень диссоциации, по­этому увеличивается число ионов. Для сильных электролитов при раз­бавлении возрастает скорость движения их ионов за счет ослабления торможения ионами противоположного знака (эффект возникает потому, что ион движется в одну сторону, а противоположно заряженная ионная атмосфера - в другую).

В дальнейшем и для слабых, и для сильных электролитов уменьшается, т.к. с разбавлением уменьшается концентрация ионов в растворе.

Более удобной для расчетов величиной является молярная электрическая проводимость. Она обозначается буквой λ_V, (лямбда).

Численно молярная электрическая проводимость равна электро­проводности раствора, содержащего 1 моль эквивалента вещества и находящегося между электродами, отстоящими друг от друга на 1 м.

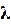
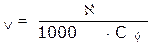
где λ_V - молярная электрическая проводимость,

С_э - молярная концентрация эквивалента или нормальная концен­трация раствора.

Зависимость молярной электрической проводимости от раз­бавления представлена на следующем рисунке (учебник Ершова, стр. 454).

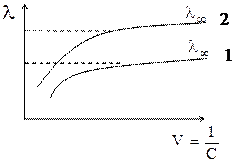1 - слабый электролит,

2 - сильный электролит,

C - молярная концентрация вещества,

V - разбавление раствора, V=1/C.

Как у сильных, так и у слабых электролитов λ, с разбавлением рас­твора возрастает и достигает максимального значения, которое называется предельной электрической проводимостью и обозначается λ_∞. Это объясняется тем, что 1 моль эквивалента вещества содержится во все воз­растающем объеме. При -этом в растворах сильных электролитов межионное взаимодействие становится очень слабым, и ионы не препятству­ют движению друг друга. Скорость движения ионов достигает предельных значения, поэтому λ, перестает зависеть от разбавления и становится постоянной величиной. В растворах слабых электролитов λ, увеличивает­ся ври разбавлении, т.к. α → 1 и увеличивается количество ионов, обра­зуемых 1 моль электролита при данной температуре. Когда степень дис­социации достигает предельного значения, равного единице, дальнейшее разбавление не приводит к росту числа ионов в растворе.

Кольрауш установил, что при малых концентрациях, т.е. больших разведениях, катионы и анионы перемещаются независимо друг от друга.

Закон Кольрауша. Предельная молярная электрическая проводи­мость раствора электролита равна сумме молярных подвижностей анионов l _A и катионов l _K, входящих в состав этого электролита.

λ_∞ = l_A + l_K

Значения молярных подвижностей ионов, входящих в состав био­логических систем, приводятся в соответствующих таблицах (учебник Ершова, стр. 459).

Ион	l∙10^4 Ом^-1∙м^2/моль
H^+	349,8
Na^+	50,1
K^+	73,5
½ Ca^2+	59,5
½ Fe^2+	53,5
½ Cu^2+	53,6
OH^-	198,3
Cl^-	76,3
I^-	78,8
CH3COO^-	40,9
H2PO4^-	36,0
HCO3^-	44,5

С помощью этих таблиц можно рассчитать λ_∞ зная, из каких ио­нов состоит электролит, например:

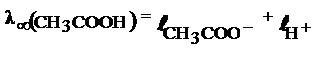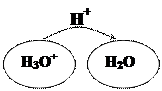
Самые высокие подвижности имеют ионы H⁺ и OH^-.

Это объясняет­ся особенностями перемещения

этих ионов в растворе. Предполагается, что

ионы H⁺ и OH^- перемещаются по "эстафетному"

механизму. Схема­тично движение протона можно показать так:

В воде протон гидратирован. H⁺ скачкообразно движется от иона H₃O⁺ к молекуле воды и т.д.

Движение гидроксид-иона можно представить так:

От молекулы воды отрывается протон H⁺, перескакивает на ион OH^-, а ион OH^-, оставшийся от воды, перемещается в обратную сторону. Но ионы. OH^- движутся медленнее, чем коны H⁺, т.к. отрыв H⁺ от молеку­лы воды, происходит труднее, чем от иона гидроксония H₃O⁺. Другие катионы и анионы имеют меньшую подвижность, чем ионы H⁺ и OH^-.

Кондуктометрия.

Дата добавления: 2014-01-06