Центр тяжести

Сила тяжести – равнодействующая сил притяжения к Земле, она распределена

по всему объёму тела. Силы притяжения, приложенные к частицам твёрдого

тела, образуют систему сил, линии, действия которых сходятся в центре

Земли. Поскольку радиус Земли значительно больше размеров любого

земного тела, силы притяжения можно считать параллельными.

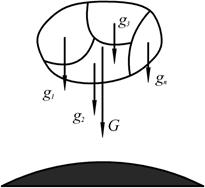
Рис. 1.48

Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:

Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси.

Изображаем тело, составленное из нескольких частей - силы тяжести частей, приложены в центрах тяжести частей.

Пусть равнодействующая (сила тяжести всего тела) – приложена в неизвестном пока центре .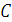

– координаты центра тяжести .

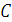– координаты центров тяжести частей тела.

Рис. 1.49

Из теоремы Вариньона следует:

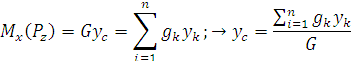
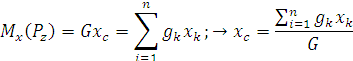
В однородном теле сила тяжести пропорциональна объёму :

,

– вес единицы объёма

Следовательно, в формулах для однородных тел:

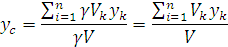
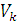– объём элемента тела

– объём всего тела

Центр тяжести однородных плоских тел (плоских фигур).

Для плоских тел можно записать:

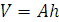, где 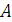– площадь фигуры, – её высота.

Тогда после подстановки в записанные выше формулы получим

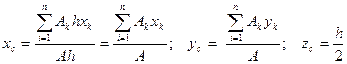
– площадь части сечения

– координаты центра тяжести частей сечения

Выражение – называют статическим моментом площади относительно оси y.

Аналогично 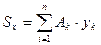– статический момент относительно оси х.

Тогда координаты центра тяжести сечения можно выразить:

Оси, проходящие через центр тяжести, называются центральными. Статический момент относительно центральной оси равен нулю.

Положение центра тяжести простых геометрических фигур:

Рис.1.50

При решении задач необходимо учесть:

1. Центр тяжести симметричных фигур находятся на оси симметрии.

2. Сложные сечения разделяем на несколько простых.

3. Полости (отверстия)рассматриваются как часть сечения с отрицательной площадью.

Пример. Необходимо определить центр тяжести представленного сечения.

Рис.1.51

Разбиваем сечение на простейшие геометрические фигуры (прямоугольник, треугольник, половина круга).

Площадь прямоугольника

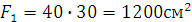
Площадь треугольника

Площадь половины круга

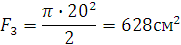
Центр тяжести:

прямоугольника

треугольника

половины круга

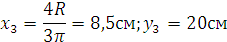
Положение центра тяжести, представленного сечения определяем по формуле

.

.

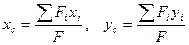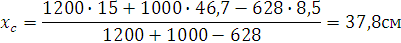
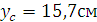РАЗДЕЛ ВТОРОЙ

Дата добавления: 2014-01-06