Уравнения равнопеременного вращения тела

Уравнения равномерного вращения тела

Вращение тела с постоянной угловой скоростью называется равномерным

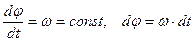
Проинтегрируем

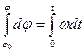
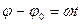
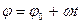– уравнение равномерного вращения тела.

Вращение тела, при котором угловое ускорение постоянно, называется равнопеременным вращением.

Если величина 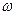увеличивается, то вращение называется равноускоренным, если уменьшается – равнозамедленным.

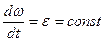
Разделим переменные:

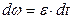
Проинтегрируем:

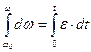
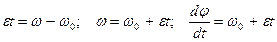
Разделим переменные:

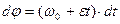
Проинтегрируем:

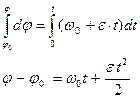
В результате получим: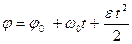

В общем случае:

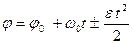– уравнение равнопеременного движения.

Знак «+» – соответствует ускоренному вращению,

«–» – замедленному.

3.2.1.Скорость и ускорение точки твердого тела, вращающегося вокруг неподвижной оси.

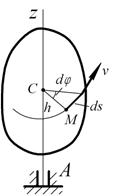Рассмотрим точку М, находящуюся на расстоянии h от оси вращения Аz.

При вращении точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна к оси вращения, а центр С лежит на самой оси. Если за время 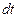происходит элементарный поворот тела на угол 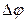, то точка М при этом совершит вдоль своей траектории элементарное перемещение 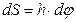. Тогда скорость точки будет равна

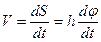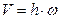Рис. 2.10 или (21)

Скорость 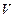называют еще линейной или окружной скоростью точки М.

Направлена линейная скорость по касательной к описываемой точкой М окружности.

Как следует из формулы, линейные скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения.

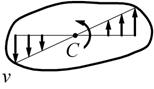
Рис. 2.11

Для нахождения ускорения точки М воспользуемся формулами:

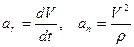
В нашем случае 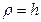. Подставляя сюда значение 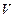, получим:

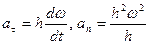
или окончательно

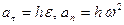
Касательное ускорение 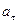направлено по касательной к траектории (в сторону движения, если тело вращается ускоренно или в обратную, если тело вращается замедленно); нормальное 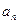всегда направлено по радиусу h к оси вращения.

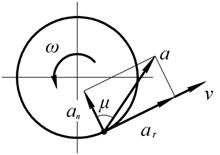
Рис. 2.12

Полное ускорение точки М будет равно

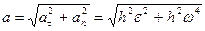или

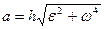(23)

Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом 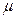, который вычисляется по формуле

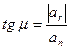
Подставляя сюда значения 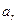и 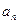, получаем:

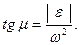
Дата добавления: 2014-01-06