Прямолинейное движение точки

Дифференциальные уравнения движения точки и их интегрирование.

Из кинематики известно, что при прямолинейном движении скорость и ускорение точки все время направлены вдоль одной и той же прямой. Так как направление ускорения совпадает с направлением действия силы, то отсюда следует, что свободная материальная точка будет двигаться прямолинейно тогда, когда действующая на нее сила имеет постоянное направление, а скорость точки в начальный момент равна нулю или направлена вдоль силы.

Рассмотрим материальную точку, движущуюся прямолинейно под действием приложенной к ней силы .

Положение точки на траектории определяется ее координатой х. Основная задача динамики в этом случае состоит в том, чтобы, зная

Рис. 3.1 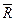, найти закон движения точки, то

есть .

Связь между х и R дает уравнение (3). Проектируя обе его части на х, получим

так как ,

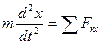(6)

Уравнение (6) называется дифференциальным уравнением прямолинейного движения точки.

Часто уравнение (6) бывает удобнее заменить двумя дифференциальными уравнениями, содержащие первые производные:

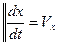(7)

(7^/)

В тех случаях, когда при решении задачи надо искать зависимость скорости от координаты х, а не от времени t (когда сами силы зависят от х) уравнение (7) преобразуют к переменному х. Так как , то

(8)

Решение основной задачи динамики сводится к тому, чтобы из данных уравнений зная силы, найти закон движения, то есть . Для этого надо проинтегрировать соответствующее дифференциальное уравнение.

Входящие в уравнение (6) силы могут зависеть от времени t, от положения точки, то есть х и от ее скорости, то есть . Следовательно, в общем случае уравнение (6) с математической точки зрения представляет дифференциальное уравнение второго порядка.

(9)

После того как с помощью тех или иных математических приемов уравнение (9) будет проинтегрировано, в полученное решение войдут две постоянные интегрирования С₁ и С₂ и общее решение будет иметь вид:

(10)

Постоянные С₁ и С₂ определяют, используя начальные условия.

Дата добавления: 2014-01-06