
- Р Р‡.МессенРТвЂВВВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВВВнокласснРСвЂВВВВВВВВРєРСвЂВВВВВВВВ
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВВРЎР‚
- LiveJournal
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Момент импульса и закон его сохранения
|
|
|
|
Рассмотрим малый элемент твердого тела - материальную точку массой 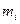 . Ее скорость
. Ее скорость 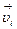 и, соответственно, импульс
и, соответственно, импульс 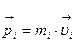 направлены по касательной к траектории точки (окружности радиусом
направлены по касательной к траектории точки (окружности радиусом 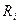 ).
).
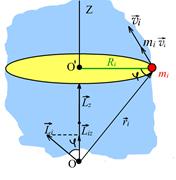 Рис.4.6
Рис.4.6
| Вектором момента импульса 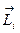 материальной точки относительно неподвижной точки материальной точки относительно неподвижной точки 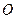 называется физическая величина, определяется векторным произведением: называется физическая величина, определяется векторным произведением:
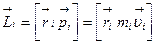 . (1.4.13)
Вектор . (1.4.13)
Вектор 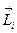 проходит через точку проходит через точку 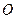 , его направление определяется правилом векторного произведения векторов, а модуль равен: , его направление определяется правилом векторного произведения векторов, а модуль равен: 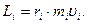 (1.4.14) (1.4.14)
|
Вектор момента импульса 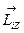 материальной точки относительно оси
материальной точки относительно оси 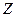 , представляет собой проекцию на эту ось вектора
, представляет собой проекцию на эту ось вектора 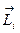 . Он лежит на оси вращения и не имеет определенной точки приложения, его модуль определяется выражением
. Он лежит на оси вращения и не имеет определенной точки приложения, его модуль определяется выражением
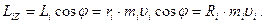 (1.4.15)
(1.4.15)
Вектор момента импульса 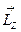 твердого тела относительно
твердого тела относительно 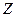 равен сумме векторов
равен сумме векторов 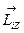 всех его точек. Все векторы
всех его точек. Все векторы 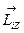 лежат на оси вращения и направлены в одну сторону, поэтому и результирующий вектор
лежат на оси вращения и направлены в одну сторону, поэтому и результирующий вектор 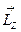 лежит на оси
лежит на оси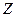 , его модуль равен:
, его модуль равен:
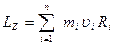
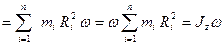 . (1.4.16)
. (1.4.16)
Уравнение (1.4.16) можно записать в векторной форме: 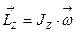 . (1.4.17)
. (1.4.17)
Продифференцировав (1.4.17) по времени (при 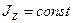 ), получим:
), получим:
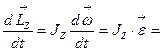
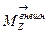 . (1.4.18)
. (1.4.18)
Это еще одна форма записи основного уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная по времени от момента импульса 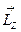 твердого тела относительно оси вращения равна моменту внешних сил
твердого тела относительно оси вращения равна моменту внешних сил 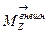 , действующих на тело, относительно той же оси.
, действующих на тело, относительно той же оси.
Последнее уравнение можно записать в виде: 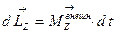 (1.4.19)
(1.4.19)
изменение момента импульса вращающегося тела происходит под действием импульса момента внешних сил, действующих на него.
В замкнутой системе момент внешних сил 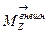 равен нулю. Поэтому
равен нулю. Поэтому
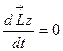 и
и 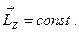 (1.4.20)
(1.4.20)
Это выражение представляет собой закон сохранения момента импульса: момент импульса замкнутой системы относительно неподвижной оси сохраняется, т. е. не изменяется с течением времени.
Это фундаментальный закон природы. Он является следствием изотропности пространства, т. е. одинаковости свойств пространства по всем направлениям. Поворот замкнутой системы как целого не изменяет ее механических свойств.
Поскольку 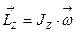 , то для замкнутых систем
, то для замкнутых систем 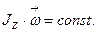 (1.4.21)
(1.4.21)
 Рис.4.7
Рис.4.7
| Это значит, что если момент инерции тела не изменяется (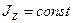 ), то тело вращается с постоянной скоростью ( ), то тело вращается с постоянной скоростью (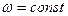 ). Если величина ). Если величина 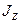 изменяется, то и величина изменяется, то и величина 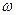 тоже должна изменяться. Если тоже должна изменяться. Если 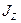 увеличивается, то увеличивается, то 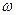 должна уменьшаться и наоборот. Качественным подтверждением закона сохранения момента импульса может служить опыт со скамьей Жуковского (рис.4.7) - горизонтальной площадкой, имеющей форму круга и свободно вращающейся без трения должна уменьшаться и наоборот. Качественным подтверждением закона сохранения момента импульса может служить опыт со скамьей Жуковского (рис.4.7) - горизонтальной площадкой, имеющей форму круга и свободно вращающейся без трения
|  Рис.4.8
Рис.4.8
|
вокруг вертикальной оси 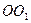 . Человек с гантелями в руках стоит в центре скамьи. Момент внешних сил равен нулю. Скамью приводят во вращение с угловой скоростью
. Человек с гантелями в руках стоит в центре скамьи. Момент внешних сил равен нулю. Скамью приводят во вращение с угловой скоростью 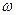 , когда человек держит гантели на вытянутых в стороны руках. Если он поднесет гантели к груди, то скорость вращения скамьи заметно возрастет, при разведении рук вновь уменьшится. Изменяя положение рук, человек меняет момент инерции своего тела.
, когда человек держит гантели на вытянутых в стороны руках. Если он поднесет гантели к груди, то скорость вращения скамьи заметно возрастет, при разведении рук вновь уменьшится. Изменяя положение рук, человек меняет момент инерции своего тела.
Из закона сохранения (1.4.21) следует, что внутренние силы не могут изменить момент импульса тела или системы тел. Однако, они могут вызвать вращение частей внутри системы. Подтверждает это следующий опыт (рис.4.8). Путь человек стоит на скамье Жуковского и держит над головой насаженное на палку неподвижное велосипедное колесо. Момент импульса этой системы относительно оси вращения равен нулю. Если привести колесо во вращение, то скамья начнет вращаться в противоположную сторону. Момент импульса системы по-прежнему равен нулю. Если повернуть палку с вращающимся колесом вниз, то направление вращения скамьи изменится на противоположное.
В табл. 4.2 приведены основные величины и уравнения, описывающие поступательное движение тела и его вращение вокруг неподвижной оси.
Таблица 4.2
| Поступательное движение | Вращательное движение | ||
| Масса | 
| Момент инерции | 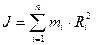
|
| Сила | 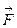
| Момент силы | 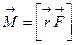 ; ;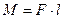
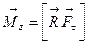 ; ; 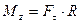
|
| Импульс | 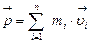
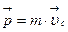
| Момент импульса | 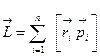
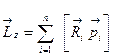 ; ;
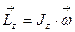
|
| Основное уравнение динамики | 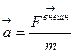
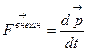
| Основное уравнение динамики |  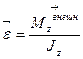
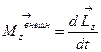
|
| Работа | 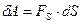
| Работа | 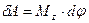
|
| Кинетическая энергия | 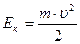
| Кинетическая энергия | 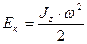
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 416; Нарушение авторских прав?; Мы поможем в написании вашей работы!