Уравнение состояния идеального газа

Идеальным считается газ, который можно рассматривать как систему невзаимодействующих материальных точек, упруго сталкивающихся друг с другом и со стенками сосуда.

Уравнение состояния представляет собой функциональную зависимость, связывающую между собой термодинамические параметры: .

Экспериментально установлено, что для 1 моля идеального газа выполняется уравнение Клапейрона (уравнение состояния 1 моля идеального газа) 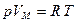, (2.1.3)

где 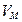– молярный объем (объем 1 моля) газа; 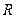– универсальная газовая постоянная. Универсальность 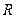вытекает из закона Авогадро, согласно которому при одинаковых давлениях и температурах молярные объемы различных газов одинаковы. Подставив в это уравнение значения 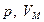и , соответствующие нормальным условиям, получим значение универсальной газовой постоянной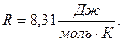

От уравнения состояния 1моля легко перейти к уравнению для любой массы 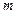газа. При одинаковом давлении и температуре молей газа будут занимать в раз больший объем, чем один моль: . Умножив обе части уравнения Клапейрона на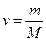

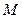(– молярная масса газа) и заменив 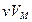на 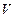, получим уравнение состояния идеального газа (уравнение Менделеева – Клапейрона) 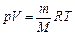. (2.1.4)

Разделим обе части уравнения Клапейрона на число Авогадро 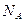(число частиц, содержащихся в 1 моле) 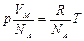или ,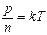

где 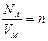– концентрация молекул (число частиц газа, содержащихся в единичном объеме); 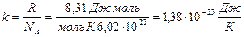– постоянная Больцмана.

Следовательно, при постоянной температуре давление газа прямо пропорционально концентрации его молекул 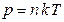. (2.1.5)

Это еще одна форма записи уравнения состояния идеального газа.

Выясним физический смысл универсальной газовой постоянной .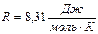

Рис.1.1

Пусть в цилиндре под поршнем находится 1 моль газа, с параметрами состояния 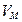, 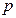и . При нагревании на газ, изобарически расширяясь, сдвинет поршень на расстояние 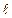. Следовательно, сила 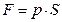, действующая на поршень с площадью поперечного сечения , совершит работу , (2.1.6)

где 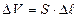– изменение объема газа.

После нагревания газ займет объем давление его не изменится. Запишем уравнения состояния 1 моля газа до нагревания и после него:

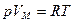и .

Вычтем из второго уравнения первое: . (2.1.7)

Выражения (2.1.5) и (2.1.7) совпали. Следовательно, универсальная газовая постоянная численно равна работе, которую совершает 1 моль идеального газа изобарически расширяясь при нагревании на .

Дата добавления: 2014-01-06