Теорема Гаусса. Пусть мы имеем элементарную площадку dS,

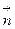Пусть мы имеем элементарную площадку dS,

a нормаль 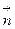к которой в месте расположения

dS 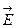площадки, составляет с вектором 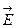угол a.

(рис. 14.5). Элементарным потоком dФ сквозь

Рис.14.5 площадку dS называют величину

dФ = E · dS · cosa = E_n dS = ·,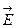

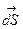где E_n - проекция вектора 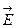на направление нормали 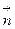к площадке, 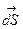- вектор, модуль которого равен dS, а направление совпадает с нормалью .

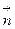Для произвольной поверхности S поток вектора 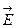сквозь нее можно записать:

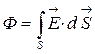. (3.3.1)

Следует отметить, что в случае замкнутых поверхностей за положительное направление нормали 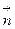берется внешняя нормаль, т.е. направленная наружу поверхности.

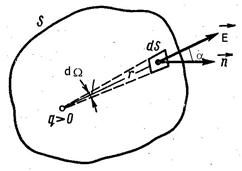Рис.14.6

Рассмотрим поле одного точечного заряда q (рис.14.6). Проведем вокруг этого заряда произвольную замкнутую поверхность и найдем поток вектора 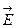сквозь площадку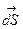

.

Подставив значение Е для точечного заряда, тогда последнюю формулу можно записать:

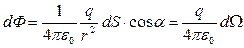, (3.3.2)

где - телесный угол, опирающийся на элемент поверхности dS с вершиной в точке расположения заряда q. Интегрируя выражение (3.3.2) по всему телесному углу мы получим 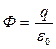и заменив левую часть этого уравнения по (3.3.1) имеем:

.

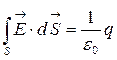Если заряд охватывает поверхность любой формы, то угол a может принимать значения больше p / 2, а значит, cosa и могут принимать значения, как больше нуля, так и меньше нуля. Отсюда следует, что если заряд расположен вне замкнутой поверхности, то поток вектора 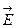через нее равен нулю. В случае, когда поле создается системой точечных зарядов q₁, q₂¼ q_n то в соответствии с принципом суперпозиции (3.2.4) 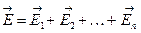поэтому:

.

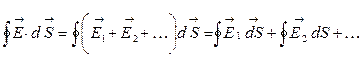Каждый интеграл в правой части равен q_i /e_о, если заряд q_i находится внутри замкнутой поверхности. Поэтому в правой части предыдущего уравнения мы должны записать алгебраическую сумму зарядов q_i, находящихся внутри поверхности S. Таким образом окончательно можно записать:

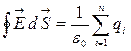. (3.3.3)

Данное уравнение математически выражает теорему Гаусса. Ее можно сформулировать так: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри данной поверхности, деленной на e₀. Если заряды распределены непрерывно с объемной плотностью 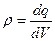, то суммарный заряд, находящийся внутри замкнутой поверхности, охватывающий объем V:

. (3.3.4)

Используя формулу (3.3.4) теорему Гаусса можно записать:

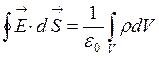. (3.3.5)

Дата добавления: 2014-01-06