Электрическая емкость

Электроемкость уединенного проводника.

Рассмотрим проводник, удаленный от других проводников, тел и зарядов в связи с чем его можно рассматривать как уединенный проводник. Из опыта следует, что между зарядом и потенциалом существует зависимость q = Сj.

Величину 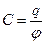(3.5.2)

называют электроемкостью или просто емкостью уединенного проводника. Эта величина численно равна заряду, сообщение которого проводнику повышает его потенциал на единицу. Емкость зависит от формы и размеров проводника и не зависит от материала, агрегатного состояния и от размеров полостей внутри проводника. Емкость также не зависит от заряда и потенциала проводника. Последнее утверждение не противоречит формуле (3.5.2). ее следует читать так, что потенциал проводника пропорционален его заряду и обратно пропорционален емкости. Попробуем найти емкость уединенного проводника, имеющего форму шара радиусом R. Для этого определим потенциал шара, использовав формулу, связывающую 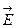и j:

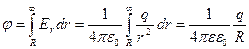. (3.5.3)

Если полученный результат подставить в формулу (3.5.2) то для С получим:

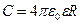. (3.5.4)

За единицу емкости в системе СИ принимают емкость такого проводника, потенциал которого изменяется на 1В при сообщении ему заряда 1Кл. Эта единица называется фарадом (Ф). Фарад - очень большая единица. Если землю рассматривать как проводящий шар радиусом 6400 км, то емкость ее равняется примерно 700×10^-6Ф. Поэтому на практике чаще приходится встречаться с емкостями мкФ = 10^-6Ф и nФ = 10^-12Ф.

Взаимная емкость. Конденсаторы.

Если к уединенному проводнику приближать другие проводники, то емкость первого проводника будет увеличиваться. Это связано с тем, что на приближающихся проводниках поле данного проводника будет вызывать перераспределение зарядов. Например, положительно заряженный проводник на приближающемся проводнике вызывает такое перераспределение, что индуцированные отрицательные заряды оказываются ближе к проводнику чем положительные. Поэтому потенциал проводника, который определяется суммой потенциала собственных зарядов и зарядов, индуцированных на других телах, уменьшится. Следовательно, его емкость по (3.5.2) увеличится таким образом можно создать систему проводников, которая будет обладать емкостью, значительно большей, чем емкость уединенного проводника. Наибольший практический интерес представляет система проводников, близко расположенных друг-другу и заряженных одинаковыми по величине, но противоположными по знаку зарядами. Такую систему называют конденсатором, а проводники – его обкладками. Емкость конденсатора определяется:

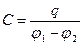, (3.5.5)

где j₁ - j₂ –разность потенциалов между обкладками, q – заряд, расположенный на положительно заряженной обкладке конденсатора. Разность потенциалов иногда называют напряжением и обозначают буквой U. Поэтому формулу (3.5.5) можно записать:

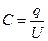. (3.5.6)

По форме обкладок конденсаторы бывают плоские, цилиндрические и сферические. Определим емкость плоского конденсатора. Пусть площадь обкладки S а заряд на ней q. Напряженность поля между обкладками, как мы ранее определили

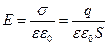. (3.5.7)

Исходя из формулы (3.4.16) разность потенциалов между обкладками

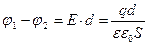, (3.5.8)

отсюда для емкости конденсатора получаем:

, (3.5.9)

где d – расcтояние между обкладками; e - диэлектрическая проницаемость среды, заполняющий зазор между обкладками. Нетрудно получить для емкости цилиндрического конденсатора формулу:

, (3.5.10)

где 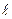- длина конденсатора, R₁ и R₂ – радиусы внутренней и наружной цилиндрических обкладок. Емкость сферического конденсатора определяется формулой:

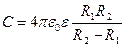, (3.5.11)

где R₁ и R₂ – радиусы внутренней и наружной обкладок. Отметим, что формулы (3.5.10) и (3.5.11) при малом зазоре между обкладками переходят в формулу (3.5.9)

Дата добавления: 2014-01-06