
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Второе уравнение Максвелла
|
|
|
|
Согласно рассмотренному выше первому уравнению Максвелла изменяющееся магнитное поле порождает вихревое электрическое поле. Максвелл считал, что электрическое и магнитное поля всегда связаны, поэтому изменяющееся со временем электрическое поле должно приводить к появлению магнитного поля.
Предположение Максвелла нашло подтверждение. Рассмотрим цепь переменного тока, содержащую конденсатор (рис.24.1).



 + -
+ -
 Iсм
Iсм






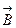
 Iпр
Iпр 







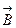 Iïð
Iïð

 А / ~ / В
А / ~ / В
Рис. 24.1
В этой цепи токи проводимости, создаваемые движущимися зарядами, текут по проводникам и отсутствуют в зазоре между обкладками конденсатора. В то же время между обкладками заряжающегося и разряжающегося конденсатора существует переменное электрическое поле, которое в каждый момент времени создает такое магнитное поле, как если бы между обкладками протекал ток проводимости силой, равной силе тока в подводящих проводах.
Чтобы установить количественные соотношения между изменяющимся электрическим полем и возникающим магнитным полем, Максвелл ввел понятие тока смещения. Током смещения Максвелл назвал переменное электрическое поле, т.к. оно создает в пространстве магнитное поле, как и любой ток. Т.к. Iпр = Iсм, то и плотность тока проводимости 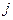 пр=
пр=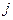 см. Плотность тока проводимости вблизи обкладок конденсатора
см. Плотность тока проводимости вблизи обкладок конденсатора
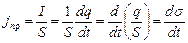 , (4.10.7)
, (4.10.7)
где 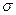 - поверхностная плотность зарядов, S- площадь обкладок. Тогда
- поверхностная плотность зарядов, S- площадь обкладок. Тогда
 .
.
Электрическое поле можно характеризовать вектором электрического смещения 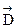 . Из электростатики известно, что электрическое смещение связано с поверхностной плотностью заряда
. Из электростатики известно, что электрическое смещение связано с поверхностной плотностью заряда 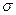 на обкладках конденсатора соотношением
на обкладках конденсатора соотношением
D=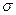 .
.
Плотность тока смещения с учетом этого соотношения равна
 . (4.10.8)
. (4.10.8)
Знак частной производной говорит о том, что магнитное поле определяется только быстротой изменения электрического смещения во времени.
Можно показать, что направление векторов 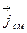 и
и 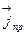
 всегда совпадают с направлением вектора
всегда совпадают с направлением вектора 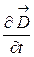 , поэтому равенство (4.10.8) можно записать в векторной форме:
, поэтому равенство (4.10.8) можно записать в векторной форме:
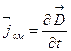 . (4.10.9)
. (4.10.9)
Токи проводимости и смещения соответственно равны
Iпр=jпр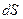 и Iсм =jсм
и Iсм =jсм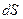 .
.
При расчете магнитных полей необходимо брать полный ток
 . (4.10.10)
. (4.10.10)
Так как
DdS = dФе,
где dФе- элементарный поток электрического смещения через площадку 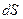 , то:
, то:
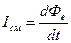 . (4.10.11)
. (4.10.11)
Введение: Понятие тока смещения и полного тока дает возможность утверждать, что все цепи переменного тока всегда замкнуты: ток проводимости обрывается на концах проводника, а в диэлектриках и вакууме между концами проводника ток смещения замыкает ток проводимости. Если полный ток равен

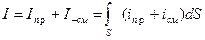 , (4.10.12)
, (4.10.12)
то теорема о циркуляции вектора напряженности может быть записана так:
 (4.10.13)
(4.10.13)
или через плотности токов проводимости и смещения в векторной форме
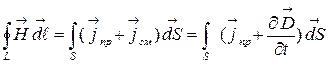 . (4.10.14)
. (4.10.14)
Это второе уравнение Максвелла, утверждающее факт появления вихревого магнитного поля при всяком изменении электрического поля. Там, где ток проводимости отсутствует (например, между обкладками конденсатора) или им можно пренебречь по сравнению с током смещения Iсм закон полного тока можно записать так
 .
.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 416; Нарушение авторских прав?; Мы поможем в написании вашей работы!