Примеры решения задач. Пример 1. Определить для серной кислоты: 1) относи­тельную молекулярную массу Мr; 2) молярную массу М

Пример 1. Определить для серной кислоты: 1) относи­тельную молекулярную массу М_r; 2) молярную массу М.

Решение. 1. Относительная молекулярная масса вещества равна сумме относительных атомных масс всех элементов, атомы которых входят в состав молекулы дан­ного вещества, и определяется по формуле

(1)

где n_i — число атомов i -гo элемента, входящих в моле­кулу; А_{r , i} — относительная атомная масса i -го элемента. Химическая формула серной кислоты имеет вид H₂SO₄. Так как в состав молекулы серной кислоты входят атомы трех элементов, то стоящая в правой части равенства (1) сумма будет состоять из трех слагаемых и эта формула примет вид

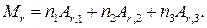(2)

Из формулы серной кислоты далее следует, что n ₁ = 2 (два атома водорода), n ₂ = 1 (один атом серы) и n ₃ = 4 (четыре атома кислорода).

Значения относительных атомных масс водорода, серы и кислорода найдем в таблице Д. И. Менделеева или в табл. 14 Приложения:

А_{r ,1} = l,  А_{r ,2} = 32,  А_{r ,3} = 16.

Подставив значения n_i и А_{r , i} в формулу (2), найдем относительную молекулярную массу серной кислоты:

M_r = 2∙1 + 1∙32 + 4∙16 = 98.

2. Зная относительную молекулярную массу М_r, най­дем молярную массу серной кислоты по формуле

М = M_rk, (3)

где k = 10^–l кг/моль.

Подставив в (3) значения величии, получим

М = 98∙10^–3 кг/моль.

Пример 2. Определить молярную массу М смеси кис­лорода массой m ₁ = 25 г и азота массой m ₂ = 75 г.

Решение. Молярная масса смеси М есть отноше­ние массы смеси т к количеству вещества смеси ν:

М = m/ν. (1)

Масса смеси равна сумме масс компонентов смеси:

т = т ₁ + m ₂.

Количество вещества смеси равно сумме количеств вещества компонентов:

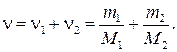
Подставив в формулу (1) выражения т и ν,получим

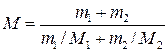(2)

Применив метод, использованный в примере 1, найдем молярные массы кислорода M ₁ и азота M ₂:

М ₁ = 32∙10^–3 кг/моль; М₂ = 28∙10^–3 кг/моль.

Подставим значения величии в (2) и произведем вы­числения:

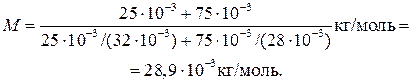
Пример 3. Определить число N молекул, содержащих­ся в объеме V = l мм³ воды, и массу т ₁ молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d мо­лекул.

Решение. Число N молекул, содержащихся в не­которой системе массой m, равно произведению постоян­ной Авогадро N _A на количество вещества ν:

N = ν N _A.

Так как ν = m/M, где М — молярная масса, то 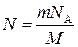. Выразив в этой формуле массу как произведение плотности на объем V, получим

N = ρ VN _A /M.

Произведем вычисления, учитывая, что М = 18∙10^–3 кг/моль (см. табл. 14 Приложения):

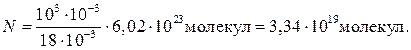
Массу m ₁ одной молекулы можно найти по формуле

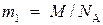(1)

Подставив в (1) значения М и N _a, найдем массу моле­кулы воды:

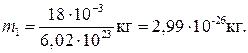
Если молекулы воды плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объем (кубическая ячейка) V ₁ = d ³, где d — диаметр мо­лекулы. Отсюда

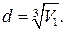(2)

Объем V ₁ найдем, разделив молярный объем V _m на число молекул в моле, т. е. на N _a:

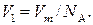(3)

Подставим выражение (3) в (2):

,

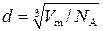где V _m = M / ρ. Тогда

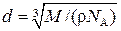
Проверим, дает ли правая часть выражения (4) единицу длины:

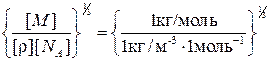
Произведем вычисления:

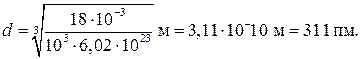
Пример 4. В баллоне объемом 10 л находится гелий под давлением р ₁ = 1 МПа и при температуре T = 300 К. После того как из баллона было взято m = 10г гелия, температура в баллоне понизилась до T = 290 К. Опре­делить давление р ₂ гелия, оставшегося в баллоне.

Решение. Для решения задачи воспользуемся уравнением Менделеева—Клапейрона, применив его к конечному состоянию газа:

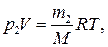(1)

где m ₂ — масса гелия в баллоне в конечном состоянии; М — молярная масса гелия; R — молярная газовая по­стоянная.

Из уравнения (1) выразим искомое давление:

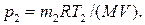
Массу m ₂ гелия выразим через массу т ₁, соответству­ющую начальному состоянию, и массу m гелия, взятого из баллона:

m ₂ = m ₁ – m.

Массу m ₁ гелия найдем также из уравнения Менде­леева-Клапейрона, применив его к начальному со­стоянию:

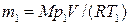. (4)

Подставив выражение массы m ₁ в (3), а затем выра­жение т ₂ в (2), найдем

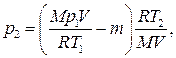
или

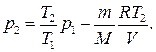(5)

Проверим, дает ли формула (5) единицу давления. Для этого в ее правую часть вместо символов величин подставим их единицы. В правой части формулы два слагаемых. Очевидно, что первое из них дает единицу давления, так как состоит из двух множителей, первый из которых (T ₂/ T ₁) — безразмерный, а второй — давле­ние. Проверим второе слагаемое:

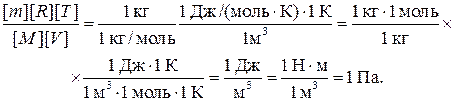
Паскаль является единицей давления. Произведем вычисления по формуле (5), учитывая, что М = 4∙10^–3 кг/моль (см. табл. 14 Приложения):

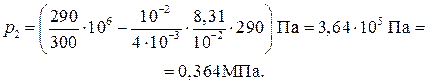
Пример 5. Баллон содержит m ₁ = 80 г кислорода и m ₂ = 320 г аргона. Давление смен р = 1 МПа, температу­ра T = 300К. Принимая данные газы за идеальные, определить объем V баллона.

Решение По закону Дальтона, давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. По уравнению Менделеева — Клапейрона, парциальные давления р ₁ кислорода и р₂ аргона выра­жаются формулами

.

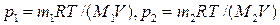Следовательно, по закону Дальтона, давление смеси газов

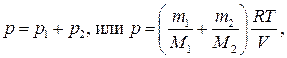
откуда объем баллона

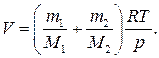
Произведем вычисления, учитывая, что M ₁ = 32∙10^–3 кг/моль, М ₂ = 40∙10^–3 кг/моль (см. табл. 14 При­ложения):

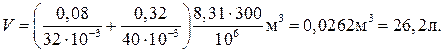
Пример 6. Найти среднюю кинетическую энергию 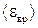вращательного движения одной молекулы кислоро­да при температуре T = 350 К, а также кинетическую энергию Е _к вращательного движения всех молекул кислорода массой m = 4г.

Решение. На каждую степень свободы молекулы газа приходится одинаковая средняя энергия 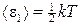, где k — постоянная Больцмана; Т — термодина­мическая температура газа. Так как вращательному движению двухатомной молекулы (молекула кислоро­да — двухатомная) соответствуют две степени свободы, то средняя энергия вращательного движения молекулы кислорода

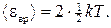(1)

Кинетическая энергия вращательного движения всех молекул газа

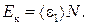(2)

Число всех молекул газа

N = N _aν, (3)

где N _A — постоянная Авогадро; ν — количество вещества. Если учесть, что количество вещества ν =m / M, где m — масса газа; М — молярная масса газа, то формула (3) примет вид

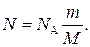
Подставив выражение N в формулу (2), получаем

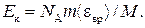(4)

Произведем вычисления, учитывая, что для кислорода M = 32∙10^–3 кг/моль (см. табл. 14 Приложения):

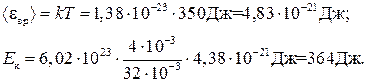
Пример 7. Вычислить удельные теплоемкости при постоянном объеме c_V и при постоянном давлении с_р неона и водорода, принимая эти газы за идеальные.

Решение. Удельные теплоемкости идеальных газов выражаются формулами

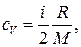(1)

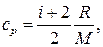(2)

где i — число степеней свободы молекулы газа; М — мо­лярная масса. Для неона (одноатомный газ) i = 3 и М = 20∙10^–3 кг/моль (см. табл. 14 Приложения). Произведем вычисления:

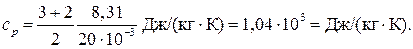
Для водорода (двухатомный газ) i = 5 и М = 2∙10^–3 кг/моль. Тогда

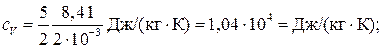
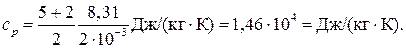
Пример 8. Вычислить удельные теплоемкости с_V и с _p смеси неона и водорода, если массовые доли неона и водорода составляют w ₁ = 80% и w ₂ = 20%. Значения удельных теплоемкостей газов взять из предыдущего примера.

Решение. Удельную теплоемкость c_V смеси при постоянном объеме найдем следующим образом. Теплоту, необходимую для нагревания смеси на Δ T выразим двумя способами:

Q = c_V (m ₁ + m ₂)Δ T, (1)

Q = (c_{V ,1} m ₁ + c_{V ,2} m ₂)Δ T, (2)

где c_{V ,1} — удельная теплоемкость неона; c_{V ,2} — удельная теплоемкость водорода.

Приравняв правые части (1) и (2) и разделив обе части полученного равенства на Δ T, получим c_V (m ₁ + m ₂) = c_{V ,1} m ₁ + c_{V ,2} m ₂. Отсюда

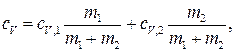
или

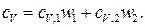
где 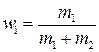и .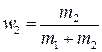

Рассуждая так же, получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:

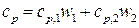
Произведем вычисления:

с_V = (6,24∙10²∙0,8 + 1,04∙10⁴.0,2) Дж/(кг∙К) =

= 2,58∙10³ Дж/(кг∙К) = 2,58 кДж/(кг∙К);

с_р = (1,04∙10³∙0,8 + 1,46∙10⁴∙0,2) Дж/(кг∙К) =

= 3,75∙10³ Дж/(кг∙К) = 3,75 кДж/(кг∙К).

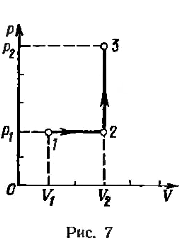
Пример 9. Кислород массой m = 2 кг занимает объем V ₁ = l м³ и находится под давлением р ₁ = 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V ₂ = 3 м, а затем при постоянном объеме до давления р ₃ = 0,5 МПа. Найти изменение Δ U внутренней энергии газа, совершенную им работу А и теплоту Q, передан­ную газу. Построить график процесса.

Решение. Изменение внутренней энергии газа

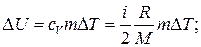(1)

где i — число степеней свободы молекул газа (для двух­атомных молекул кислорода i = 5); Δ Т = Т ₃ — Т ₁ — разность температур газа в конечном (третьем) и начальном состояниях.

Начальную и конечную температуру газа найдем из уравнения Менделеева — Клапейрона 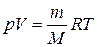, откуда

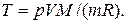
Работа расширения газа при постоянном давлении выражается формулой

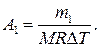
Работа газа, нагреваемого при постоянном объеме, равна нулю:

A ₂ = 0.

Следовательно, полная работа, совершаемая газом,

A = A ₁ + A ₂ = A ₁.

Согласно первому началу термодинамики, теплота Q, переданная газу, равна сумме изменения внутренней энергии Δ U и работы А:

Q = Δ U + A.

Произведем вычисления, учтя, что для кислорода М = 32∙10^–3 кг/моль (см. табл. 14 Приложения):

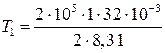К = 385 К;

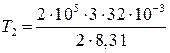К = 1155;

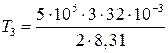К = 2887;

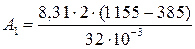Дж = 0,400∙10⁶ Дж = 0,4 МДж;

А = А ₁ = 0,4 МДж;

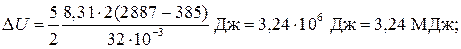
Q = (3,24 + 0,4) МДж = 3,64 МДж.

График процесса приведен на рис. 7.

Пример 10. В цилиндре под поршнем находится водород массой m = 0,02 кг при температуре T ₁ = 300 К. Водород сначала расширился адиабатно, увеличив свой объем в п ₁ = 5 раз, а затем был сжат изотермически, причем объем газа умень­шился в n ₂ = 5 раз. Найти темпера­туру в конце адиабатного расшире­ния и работу, совершаемую газом при этих процессах. Изобразить процесс графически.

Решение. Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением

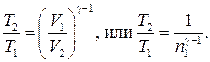
где γ — отношение теплоемкостей газа при постоянном давлении и постоянном объеме; n ₁ = V ₂/ V ₁.

Отсюда получаем следующее выражение для конечной температуры:

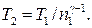
Работа А ₁ газа при адиабатном расширении может быть определена по формуле

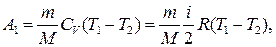
где C_V — молярная теплоемкость газа при постоянном объеме. Работа А ₂ газа при изотермическом процессе может быть выражена в виде

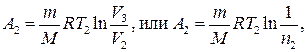
где п ₂ = V ₂/ V ₃.

Произведем вычисления, учитывая, что для водорода как двухатомного газа γ = 1,4, i = 5 и М = 2∙10^–3 кг/моль:

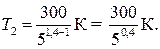
Так как 5^0,4 = 1,91 (находится логарифмированием), то

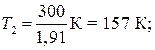
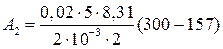Дж = 29,8кДж;

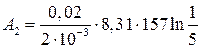Дж = –21 кДж.

Знак минус показывает, что при сжатии работа газа совершается над газом вне­шними силами.

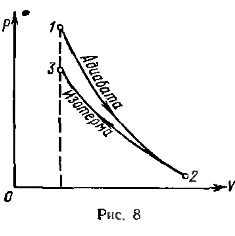График процессе приве­ден на рис. 8.

Пример 11. Тепловая ма­шина работает по обратимому циклу Карно. Температу­ра теплоотдатчика T ₁ = 500 К. Определить термический КПД η цикла и температуру Т ₂ теплоприемника тепловой машины, если за счет каждого кило­джоуля теплоты, полученной от теплоотдатчика, машина совершает работу А = 350 Дж.

Решение. Термический КПД тепловой машины показывает, какая доля теплоты, полученной от теплоотдатчика, превращается в механическую работу. Терми­ческий КПД выражается формулой

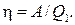
где Q ₁ — теплота, полученная от теплоотдатчика; А — работа, совершенная рабочим телом тепловой машины. Зная КПД цикла, можно по формуле η = (Т ₁ — T ₂) /T ₁ определить температуру охладителя Т ₂:

T ₂ = T ₁ (1 — η).

Произведем вычисления:

η = 350/1000 = 0,35; T ₂ = 500(1 —0,35) К = 325 К.

Пример 12. Найти добавочное давление внутри мыль­ного пузыря диаметром d = 10 cм. Какую работу нужно совершить, чтобы выдуть этот пузырь?

Решение. Пленка мыльного пузыря имеет Две сферические поверхности: внешнюю и внутреннюю. Обе поверхности оказывают давление на воздух, заключенный внутри пузыря. Так как толщина пленки чрезвычайно мала, то диаметры обеих поверхностей практически одинаковы. Поэтому добавочное давление

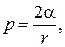
где r — радиус пузыря. Так как r = d/ 2, то

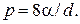
Работа, которую нужно совершить, чтобы, растягивая пленку, увеличить ее поверхность на ΔS, выражается

формулой

A = αΔ S, или  A = α(S — S ₀).

В данном случае S — общая площадь двух сферических поверхностей пленки мыльного пузыря; S ₀ — общая площадь двух поверхностей плоской пленки, затягивав­шей отверстие трубки до выдувания пузыря. Пренебре­гая S ₀, получаем

A = α S = 2π d ²α.

Произведем вычисления:

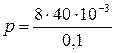Па = 3,2 Па;

A = 2∙3,14∙(0,1)²∙40∙10^–3 Дж = 2,5∙10^–3 Дж = 2,5 мДж.

Дата добавления: 2014-01-06