Теорема Остроградского-Гаусса

Любую величину векторную или скалярную, которая зависит от координат будем называть полем этой величины. Для характеристик любого векторного поля (x, y, z) пользуется величиной которая называется поток C через поверхность S

Для определения потока через поверхность S разобьём всю поверхность на бесконечно малые участки. Каждый участок настолько мал, что его можно считать плоским и считать что векторво всех участках одинаков.

90

величина которая = площади участка, а направление совпадает с направлением нормами(к этому участку

Если поверхность замкнуть, то вектор направлен наружу.

Для вычисления потока через эту поверхность надо на каждом участке вычислить скалярное произведение потом сложить

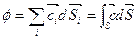
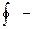интеграл через замкнутую поверхность. Определенным паток 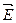через произвольную замкнутую поверхность

Для этого с начала определим поток вектора 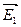напряженного поле точечного заряда

S

q

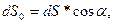где dS_0- часть сферической поверхности, радиуса R, которая видна над тем же самым телесным углом dчто и поверхность

Пусть заряд находиться вне поверхности

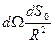
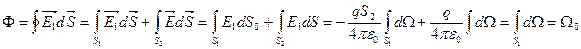
Ǿ = 0

Тогда поток этого поля, через произвольную замкнутую поверхность будет:

q_j- заряд который находиться внутри поверхности S-теорема Остроградского – Гаусса

S

Заряд, который находиться внутри поверхности S можно вычислить, если известна плотность заряда . Для этого весь объём внутри поверхности S разобьём на бесконечно малые «кубики» объёмов dV. Вычисление зарядов каждого из них по формуле , и затем сложить

dv

Получим, что заряд внутри поверхности S

v

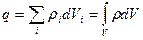
Тогда теорема Остроградского- Гаусса примет вид:

Рассмотрим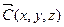

Грани кубика будем считать на столько малыми что векторна поверхности каждой из этих граней будет считаться постоянным.

Вычислим сначала поток вектор через грани 1 (x+dx)= const, x=const

Общий поток через поверхность кубика будет равен сумме этих потоков

Этот

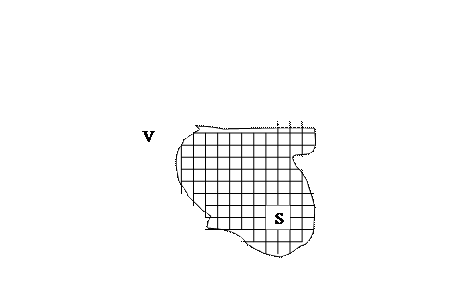
Вычислим поток вектор через произвольно замкнутую поверхность

Для этого разобьём V на бесконечное множество кубиков

Определим поток вектора каждую dv объём из этих кубиков по формуле

и затем сложим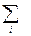

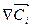
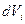
При этом надо учесть, что потоки через общую грань соседних кубиков будет в разных кубиках одинакова по величине и разные по знаку

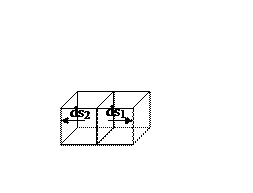
При суммирование отс потоки только через те грани кубика которые совпадают с границей потока. То есть

=

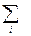
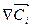
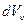математическая теория Остроградского - Гауса

С помощью теории Остроградского- Гаусса можно выяснить …… смысл…… для этого в качестве примера рассмотрим

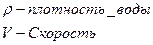
Количество воды которое протечёт через выборную поверхность

Количество воды протечёт за единицу времени

Если

Если поток вектора есть источник

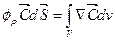
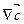
….. любового вектора определяет плотность его источника

Теория Остроградского-Гаусса

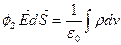
Применяет математической теории Остроградского- Гаусса

Так как это равенство должно выполняться для любого V, то из равенств интрегр, сл равенство подинтегральных выражений

Дата добавления: 2014-01-06