Лекция 19/20

Основные выводы.

1. Энтропия может быть выражена через статистический вес состояния: S = k ln W, где k — постоянная Больцмана.

Система, первоначально находившаяся в состоянии, характеризуемому малой вероятностью, будет стремиться к состоянию, характеризуемому большей вероятностью. Поэтому D S > 0.

2. Общая формулировка второго начала термодинамики:

Полная энтропия системы вместе с ее окружением в любом естественном процессе увеличивается: D S > О

3. Состояние, осуществляемое малым числом способов, называется упорядоченным. Состояние, осуществляемое многими разными способами, называется беспорядочным. Энтропию можно рассматривать как меру беспорядка в системе. Естественные процессы, при которых D S > 0, стремятся перевести систему в состояние с большим беспорядком. Например, сообщение системе тепла приводит к усилению теплового движения молекул и, следовательно, к увеличению состояния беспорядка в системе.

Из второго начала термодинамики следует, что в любом естественном (необратимом) процессе некоторое количество анергии становится недоступным, хотя, конечно, полная энергия сохраняется.

4. Электростатика — раздел физики, изучающий взаимодействие неподвижных электрических зарядов.

5. При трении некоторых веществ (например янтаря мехом) возникает явление, называемое электризацией трением. Тела приобретают электрический заряд. Существуют два вида зарядов — заряды одного и того же вида отталкиваются, заряды разных видов притягиваются. Эти два вида зарядов называют положительными и отрицательными.

6. При электризации происходит разделение зарядов на положительные и отрицательные, но их алгебраическая сумма всегда равна нулю. Поэтому был сформулирован закон сохранения электрического заряда:

Суммарный электрический заряд, возникающий в результате любого процесса, равен нулю.

7. Закон Кулона

Сила, действующая между зарядами q ₁ и q ₂, прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними.

,

где k _o — коэффициент пропорциональности.

В системе СИ единица заряда называется кулон (Кл). Величина k _o в этой системе равна k _o @ 9.10⁹ Н.м^–2/Кл. Часто употребляется величина e_о = 1/4p k _о, называемая диэлектрической проницаемостью вакуума, при этом e_о @ 8,8.10^–12.

8. Каждый электрический заряд порождает электрическое поле, заполняющее все пространство. Оно характеризуется величиной, называемой напряженностью электрического поля 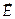: 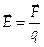. Напряженность электрического поля является векторной величиной. Поэтому электрическое поле является векторным полем.

Силовые линии поля — это линия, в каждой точке которых касательная совпадает с вектором 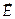, а их плотность с | 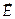|. Число силовых, пересекающих данную поверхность S, называется потоком электрического поля Ф: 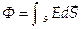. Поток Ф является скалярной величиной.

9. Теорема Гаусса:

Поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри нее зарядов деленной на e_о или умноженной на 4p k _о.

10. Примеры напряженности электрического поля для различных конфигураций распределения электрического заряда.

а) Бесконечная однородно (заряженная плоскость с плотностью заряда s = dQ/dS: 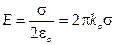и не (зависит от расстояния от плоскости.

б) Поле двух разноименно (заряженных плоскостей: внутри плоскостей и Е = 0 вне плоскостей.

в) Длинный равномерно заряженный тонкий стержень с линейной плотностью заряда l = dQ/dl: .

г) Равномерно (заряженная сферическая поверхность радиуса R

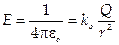при r > R: Е = 0 при r < R

д) Равномерно заряженный непроводящий шар

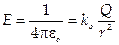при r>R; при r<R

11. Напряженность для заряженного проводящего шара радиуса R с зарядом Q:

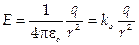при r > R E = 0 при r < R.

Заряд внутри шара, а также проводника любой формы, равен нулю. Все носители заряда располагаются на поверхности проводника.

12. Электростатические силы являются консервативными, их циркуляция равна нулю: , и потому для электрического поля можно ввести понятие потенциальной энергии U. Электрическое поле может быть охарактеризовано скалярной величиной — потенциалом j (r) º V (r) = U(r)/q, т.е. потенциальной энергией единичного заряда.

13. Электрический потенциал точечного заряда Q — это работа, которую нужно затратить, чтобы перенести единичный заряд из бесконечности на расстояние r от точечного заряда Q.

.

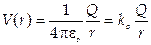Разность потенциалов между двумя точками А и В представляет собой работу, затрачиваемую при перемещении единичного заряда из одной точки в другую. V_AB = V _A – V_B. Единицей измерения электрического потенциала и разности потенциалов является вольт (В): 1 В = 1 Дж/Кл.

Дата добавления: 2014-01-06