Логические операции. В середине ХIX века Джордж Буль показал, что объекты изучаемые логикой и логические операции могут быть выражены и описаны языком математических символов

В середине ХIX века Джордж Буль показал, что объекты изучаемые логикой и логические операции могут быть выражены и описаны языком математических символов, что сводит логику к изложению схожему с алгеброй.

В настоящее время математическая логика является теоретической основой цифровой техники.

В логических устройствах аргументы – входные сигналы, логические функции – выходные сигналы.

логические переменные принимают два значения:

истина – 1;

ложь – 0.

Сложные структуры цифровых устройств основаны на том, что различные логические комбинации реализуются посредством элементарных операций, осуществляемых простыми логическими устройствами.

Аппарат алгебры логики позволяет находить схемные решения при котором число логических элементов минимально.

В булевой алгебре существует три действия над логическими переменными:

- сложение;

- умножение;

- отрицание.

1) Логическое сложение (дизъюнкция)

осуществляет функцию логического «ИЛИ»,

обозначается; +,

y=x1x2

таблица истинности

x1	x2	y

граф. обозначение

2) Логическое умножение (конъюнкция)

осуществляет функцию логического «И»,

обозначается; *,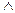

y=x1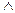x2

таблица истинности

x1	x2	y

3) Логическое отрицание (инверсия)

осуществляет функцию логического «НЕ»,

y=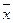 таблица истинности

x	y

Напоминание:

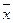+=1 – полная система событий

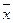*=0 – совместная система событий

Всякая более сложная логическая функция может быть построена с помощью этих трех элементарных логических функций, такая группа называется полной функциональной группой.

Пример:

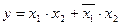
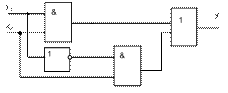
Рис. 11.2 реализация “y”

Эта полная функциональная группа (И, ИЛИ, НЕ) не является единственно возможной.

4) Элемент Шеффера

осуществляет функцию логического «И-НЕ»

Элемент Шеффера один образует полную функциональную группу.

x1	x2	y

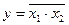таблица истинности

5) Элемент Пирса

осуществляет функцию логического «ИЛИ-НЕ»

Элемент Пирса один образует полную функциональную группу

таблица истинности

x1	x2	y

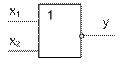
На базе элемента Шеффера или Пирса можно построить любую сложную логическую функцию (в том числе и простейшие)

Пример:

1) отрицание на элементе Шеффера.

на вход x₂ надо поставить 1.

6) «И» на элементах Шеффера.

Чтобы получить «И» надо 2 элемента «И-НЕ»

7) «ИЛИ» на элементах Шеффера.

Чтобы получить «ИЛИ» надо 3 элемента «И-НЕ» (закон де Моргана)

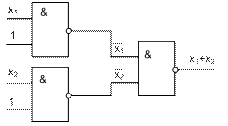
- закон де Моргана

8) Сложение по mod 2 (неравнозначность)

y=x1 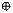x2 таблица истинности

x1	x2	y

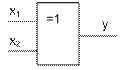
Реализации y=x1 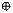x2

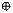y=x₁ x₂ = +

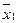
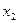
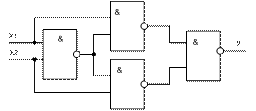
9) Логический повторитель

Дата добавления: 2014-01-06