Диффузионное уравнение

При инжекции или экстракции неосновных носителей их распределение в объеме соответствующих областей полупроводника будет неравномерным. Хаотическое тепловое движение приведет в этом случае к возникновению макроскопического процесса переноса частиц, называемого диффузией. Как известно, количество частиц, переносимых при диффузии за единицу времени через плоскость площадью s и перпендикулярную к направлению вектора градиента концентрации частиц, равно:

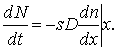(7.15)

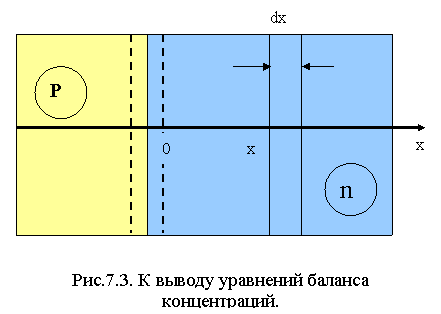
В этом уравнении: D - коэффициент диффузии, 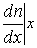-значение градиента концентрации в рассматриваемой плоскости х. Знак "-" показывает, что диффузионный перенос совершается в направлении противоположном направлению градиента концентрации(dn/dx). Рассмотрим бесконечно тонкий слой dx, n-полупроводника, параллельный плоскости p-n перехода и ограниченный плоскостями x и x+dx (рис.7.3).

Через границы х и х+dx этого слоя за единицу времени продиффундирует, соответственно

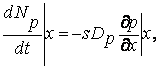(7.16)

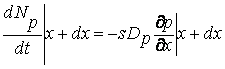(7.17)

дырок. Так как внутри слоя распределение дырок можно считать равномерным, то изменение количества дырок в слое за единицу времени можно представить как произведение объема слоя на скорость изменения концентрации дырок. С другой стороны, эта величина должна равняться разности (7.16) и (7.17). Следовательно:

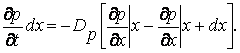(7.18)

Градиент концентрации является непрерывной функцией х, поэтому:

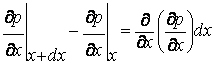(7.19)

Учитывая (7.19), уравнение баланса (7.18) можно записать в виде:

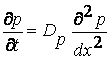(7.20)

Уравнение (7.20) носит название второго уравнения Фика.

Если в полупроводнике не происходит никаких других процессов кроме диффузии, то концентрация неосновных носителей в любом элементе объема изменяется со скоростью, пропорциональной значению второй производной от концентрации этих носителей по координате в этом элементе объема. Заметим, что коэффициенты диффузии электронных и дырочных газов, соответственно, равны:

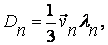
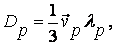(7.21)

где l_n и l_р - длины свободного пробега соответствующих носителей заряда.

Дата добавления: 2014-01-06