Главное в главе 4

На сопротивлении переменный ток совпадает по фазе с напряжением, на емкости напряжение опережает ток на 90º, на емкости ток опережает напряжение на90º. Комплексные сопротивления: - активное сопротивление, 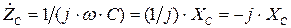- емкостное сопротивление, 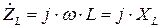- индуктивное сопротивление.

Глава 5. Последовательные соединения элементов R, L, и C. Параллельный и последовательный колебательные контуры.

Пусть катушка с активным сопротивлением R и индуктивностью L и конденсатор емкостью С включены последовательно (рис.5.1).

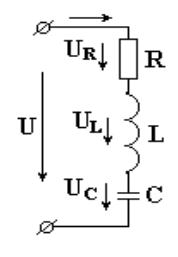
Рисунок 5.1. Последовательный колебательный контур.

В схеме протекает синусоидальный ток . Определим напряжение на входе схемы. В соответствии со вторым законом Кирхгофа: 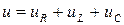, (5.1)

где , подставляя эти формулы в (5.1), получаем:

, подставляя сюда исходный синусоидальный ток i получаем:

(5.2)

Из выражения (5.2) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90º, напряжение по емкости отстает по фазе от тока на 90º. Перепишем (5.2) в комплексной форме:

(5.3)

здесь - полное комплексное сопротивление цепи, - модуль полного комплексного сопротивления, или полное сопротивление цепи, 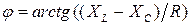- начальная фаза полного комплексного сопротивления.

При построении векторных диаграмм цепи рассмотрим три случая.

1. X_L > X_C, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока (рис.5.2).

2. Индуктивное сопротивление меньше емкостного X_L < X_C. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.5.3).

3. Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.5.4).

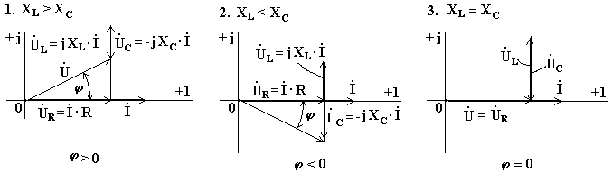
Рис. 5.2 Рис. 5.3 Рис. 5.4

Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.

(5.4)

Для возникновения резонанса необходимо, чтобы X_L=X_C при этом:

, отсюда резонансная частота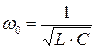

Из формулы следует, что режима резонанса можно добиться следующими способами:

1. изменением частоты;

2. изменением индуктивности;

3. изменением емкости.

В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. Последовательное соединение емкости и катушки индуктивности называется последовательным колебательным контуром. В последовательном контуре значения напряжений на емкости и индуктивности может достигать значений значительно больших входного напряжения, поэтому говорят, что в последовательном колебательном контуре имеет место резонанс напряжений.

Параллельное соединение активного сопротивления, индуктивности и емкости.

К схеме на рис. 5.5 подключено синусоидальное напряжение 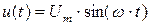. Схема состоит из параллельно включенных индуктивности L, емкости C и активного сопротивления R. Определим ток на входе схемы.

Рисунок 5.5. Параллельный колебательный контур.

В соответствии с первым законом Кирхгофа: 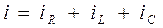, где 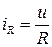, , 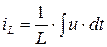, отсюда:

(5.5)

где 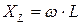- индуктивное сопротивление, 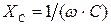- емкостное сопротивление, R - активное сопротивление

Из уравнения (5.5) видно, что ток в ветви с индуктивностью отстает по фазе от напряжения на 90º, ток в ветви с активным сопротивлением совпадает по фазе с напряжением, ток в ветви с емкостью опережает по фазе напряжение на 90º. Запишем уравнение (5.5) в комплексной форме.

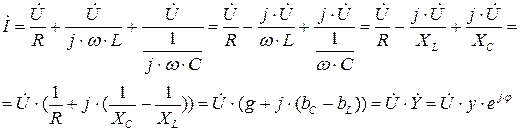(5.6)

здесь - активная проводимость, - емкостная проводимость, 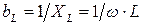- индуктивная проводимость, - полная комплексная проводимость, 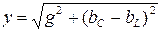- полная проводимость, - начальная фаза полной комплексной проводимости. Построим векторные диаграммы, соответствующие комплексному уравнению (5.6) рис 5.6, 5.7, 5.8.

Рис. 6.13 Рис. 6.14 Рис. 6.15

В параллельном колебательном контуре возникает резонанс токов. Резонанс токов возникает тогда, когда индуктивная и емкостная проводимости одинаковы. При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением. Из условия возникновения резонанса 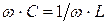получаем формулу для резонансной частоты:

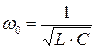, следует заметить, что формулы для резонансной частоты для последовательного и параллельного колебательного контуров одинаковы.

В режиме резонанса полная проводимость цепи минимальна, а полное сопротивление 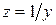максимально. Ток в неразветвленной части схемы в резонансном режиме имеет минимальное значение. В идеализированном случае R =0 и полное сопротивление равно бесконечности, в этом случае ток в неразветвленной части схемы равен нулю. Такая схема называется фильтр - пробкой.

Главное в главе 5

Последовательное и параллельное соединение емкости и индуктивности называется, соответственно, последовательным и параллельным колебательным контуром. Колебательным контурам свойственно явление резонанса - явление резкого увеличения амплитуды колебаний тока или напряжения при совпадении частоты питающего схему тока или напряжения с резонансной частотой контура. Резонансная частота одинакова для последовательного и параллельного колебательных контуров. В последовательном колебательном контуре наблюдается резонанс напряжений, в параллельном колебательном контуре - резонанс токов.

Глава 6. Мощность в цепях переменного тока.

Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток. Пусть мгновенные напряжение и ток определяются по формулам:

(6.1)

Тогда мгновенная мощность:

(6.2)

Среднее значение мгновенной мощности за период:

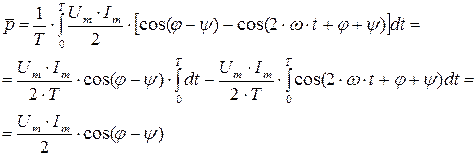(6.3)

такт как из треугольника сопротивлений

Получаем:

(6.4)

где I_D, U_D - действующее значения переменного тока и напряжения, z - полное сопротивление.

Среднее значение мгновенной мощности за период называют активной мощностью и обозначают буквой P. В системе СИ активная мощность измеряется в Ваттах (Вт). Эта мощность измеряется в ваттах и характеризует необратимое преобразование электрической энергии в другой вид энергии, например, в тепловую, световую и механическую энергию.

Возьмем реактивный элемент (индуктивность или емкость). Активная мощность в этом элементе , так как напряжение и ток в индуктивности или емкости различаются по фазе на 90º. В реактивных элементах отсутствуют необратимые потери электрической энергии, не происходит нагрева элементов. В реактивных элементах происходит обратимый процесс в виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.

Преобразуем выражение 6.2:

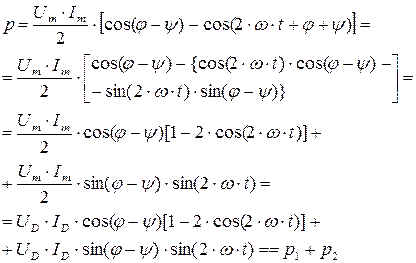(6.5)

где - мгновенная мощность на активном сопротивлении, - мгновенная мощность на реактивном элементе (индуктивности или емкости). Максимальное или амплитудное значение мощности p₂ называется реактивной мощностью:

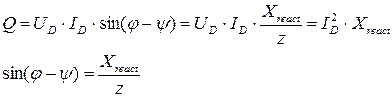(6.6)

где X_react - реактивное сопротивление (индуктивное или емкостное).

Реактивная мощность Q, измеряемая в вольтамперах реактивных (ВАР), расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.

Амплитудное значение суммарной мощности p = p₁ + p₂ называется полной мощностью. Полная мощность, измеряемая в вольтамперах (ВА), равна произведению действующих значений напряжения и тока:

(6.7)

где z - полное сопротивление цепи.

Полная мощность характеризует предельные возможности источника энергии. В электрической цепи можно использовать часть полной мощности (активную мощность):

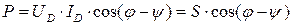(6.8)

Далее предположим, что разность фаз между напряжением и током , тогда и

(6.9)

Величина

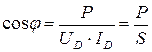(6.8)

называется коэффициентом мощности или "косинус фи". Коеффициент мощности характеризует полезную мощность, используемую потребителем.

Возьмем треугольник сопротивлений и умножим его стороны на квадрат тока в цепи. Получим треугольник мощностей (рис. 6.1).

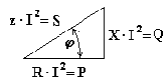
Рисунок 6.1. Треугольник мощностей.

Из треугольника мощностей получим ряд формул:

(6.9)

При анализе электрических цепей методом комплексных амплитуд используют выражения для комплексной мощности равное произведению комплексной амплитуды напряжения на комплексно сопряженную комплексную амплитуду тока тока:

(6.10)

Активная мощность всегда положительна. Реактивная мощность в цепи, имеющей индуктивный характер, - положительна, а в цепи с емкостным характером - отрицательна.

Баланс мощностей для цепей переменного тока в комплексной форме выглядит следующим образом:

(6.11)

где P_S, Q_S - активная и реактивная мощность источника, 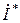- комплексная амплитуда полного тока, втекающего в цепь, P_N и Q_N - полные активная и реактивная мощности элементов цепи, P_R - активная мощность сопротивления, Q_C - реактивная мощность емкости, Q_L - реактивная мощность индуктивности, 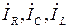- комплексные амплитуды тока, соответственно, на сопротивлении, емкости и индуктивности. Для получения полных активных и реактивных мощностей цепи надо сложить соответствующие мощности на отдельных элементах:

Глава 7. Основные понятия о магнитных цепях, ферромагнетмзм. Потери в стали. Вихревые токи.

Как известно из курса физики, вокруг проводника с током появляется магнитное поле. Интенсивность магнитного поля характеризуется векторной величиной: напряженностью магнитного поля , измеряемой в амперах на метр (A/м). Интенсивность магнитного поля характеризуется также вектором магнитной индукции 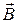, измеряемой в теслах (Тл). Напряженность магнитного поля не зависит, а магнитная индукция зависит от свойств окружающей среды.

(7.1)

где 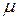-магнитная проницаемость вещества, Генри/м (Гн/м), 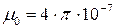Гн/м - магнитная проницаемость ваккума.

В зависимости от величины относительной магнитной проницаемости, все вещества делятся на три группы.

1. К первой группе относятся диамагнетики: вещества, у которых μ < 1.
2. Ко второй группе относятся парамагнетики, вещества с μ >1.
3. К третьей группе относятся ферромагнетики, вещества с μ >> 1.

К ферромагнетикам принадлежат железо, никель, кобальт и многие сплавы из неферромагнитных веществ.

Магнитной цепью называется совокупность устройств, содержащих ферромагнитные вещества. Процессы в магнитных цепях описываются с помощью понятий магнитодвижущей силы, магнитного потока.

Магнитным потоком называется поток вектора магнитной индукции через поверхность S:

(7.2)

Магнитный поток измеряется в веберах (Вб).

Источником магнитодвижущей силы является либо постоянный магнит, либо электромагнит (катушка, обтекаемая током). Магнитодвижущая сила электромагнита:

(7.3)

где I - ток, протекающий в катушке, W - число витков катушки.

В магнитных цепях используется свойство ферромагнитного материала тысячекратно усиливать магнитное поле катушки с током за счет собственной намагниченности.

Поместим ферромагнитный материал внутри катушки с током. Сначала, с увеличением напряженности намагничивающего поля, магнитная индукция быстро возрастает. Затем, из-за насыщения материала, при дальнейшем увеличении напряженности магнитного поля магнитная индукция почти не меняется. При уменьшении напряженности намагничивающего поля кривая размагничивания не совпадает с кривой намагничивания из-за явления гистерезиса. Явление гистерезиса заключается в том, что изменение магнитной индукции запаздывает от изменения намагничивающего поля. Кривая зависимости B(H), получающаяся при циклическом перемагничивании ферромагнитного материала, называется петлей гистерезиса. Эта кривая изображена на рис. 7.1. Чем больше площадь петли, тем больше потери на перемагничивание, нагревающие материал.

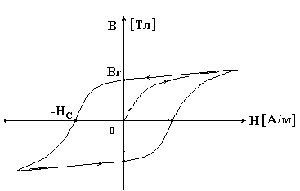
Рисунок 7.1. Кривая гестерезиса.

Значение магнитной индукции при напряженности намагничивающего поля, равном нулю, называется остаточной магнитной индукцией B_r, или остаточной намагниченностью.

Напряженность магнитного поля Н_С при В = 0 называется коэрцитивной силой.

Ферромагнитные материалы с большим значением коэрцитивной силы (H_С > 4000 А/м) называются магнитотвердыми. Из этих материалов изготавливают постоянные магниты.

Ферромагнитные материалы с малым значением коэрцитивной силы (H_С < 4000 А/м) называются магнитомягкими. Эти материалы используют в магнитопроводах электрических машин и трансформаторов.

Таким образом, зависимости B = f(H) у ферромагнитных материалов нелинейные. Эти зависимости приводятся в справочниках в табличной форме или в виде кривых, называемых кривыми намагничивания.

Основным законом, используемым при расчетах магнитных цепей, является закон полного тока:

(7.4)

Он формулируется следующим образом: линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, охватываемых этим контуром. Если контур интегрирования охватывает катушку с числом витков W, через которую протекает ток I, то алгебраическая сумма токов , где F - магнитодвижущая сила.

Обычно контур интегрирования выбирают таким образом, чтобы он совпадал с силовой линией магнитного поля, тогда произведение векторов в формуле (7.4) можно заменить произведением скалярных величин H ·и dl. В практических расчетах интеграл заменяют суммой и выбирают отдельные участки магнитной цепи таким образом, чтобы H₁, H₂,... вдоль этих участков можно было считать приблизительно постоянными. При этом (7.4) переходит в

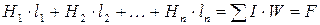(7.5)

где l₁, l₂... l_n - длины участуов магнитной цепи, H₁·l₁, H₂·l₂ … H_n·l_n - магнитные напряжения участков цепи. Магнитным сопротивлением участка магнитной цепи называется отношение магнитного напряжения рассматриваемого участка к магнитному потоку в этом участке:

(7.6)

где S - площадь поперечного сечения участка магнитной цепи, l - длина участка.

Рассмотрим расчет магнитной цепи, изображенной на рис. 7.2.

Ферромагнитный магнитопровод имеет одинаковую площадь поперечного сечения S, l_ср - длина средней силовой линии магнитного поля в магнитопроводе, δ - толщина воздушного зазора. На магнитопроводе размещена обмотка, по которой протекает ток I.

Рисунок 7.2. Магнитная цепь

Прямая задача расчета магнитной цепи заключается в том, что задан магнитный поток Ф и требуется определить магнитодвижущую силу F. Определим магнитную индукцию в магнитопроводе:

(7.7)

По кривой намагничивания найдем значение напряженности магнитного поля H, соответствующее величине В. Напряженность магнитного поля в воздушном зазоре:

(7.8)

Магнитодвижущая сила обмотки:

(7.9)

При обратной задаче расчета магнитной цепи по заданному значению магнитодвижущей силы требуется определить магнитный поток. Расчет такой задачи выполняется с помощью магнитной характеристики цепи F = f(Ф). Для построения такой характеристики необходимо задаться несколькими значениями Ф и найти соответствующие значения F. С помощью магнитной характеристики по заданной магнитодвижущей силе определяется магнитный поток.

Глава 8. Трансформаторы. Режим работы трансформатора. Основные параметры. Выбор типа трансформатора. Коэффициент мощности.

Трансформатор представляет собой электромагнитный аппарат, предназначенный для преобразования величин токов и напряжений без изменения частоты. Трансформатор состоит из замкнутого ферромагнитного сердечника, на котором размещены две или большее число обмоток. Обмотка, подключенная к источнику энергии, называется первичной. Обмотки, подключенные к сопротивлениям нагрузки, называются вторичными. Сердечник (магнитопровод) трансформатора изготавливают из листовой электротехнической стали, имеющей малые потери на перемагничивание и на вихревые токи. Отдельные листы стали изолируют слоем лака, после чего стягивают болтами. Такое устройство применяется для уменьшения вихревых токов, индуктируемых в стали переменным потоком.

По конструкции сердечника различают два типа трансформатора: броневые и стержневые. На рис. 10.1 изображен броневой трансформатор, или трансформатор с Ш-образным сердечником, а на рис. 10.2 - стержневой трансформатор с П-образным сердечником.

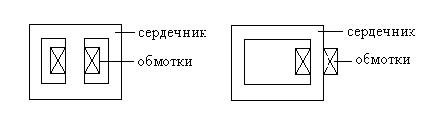
Рис. 8.1 Рис. 8.2

Под холостым ходом трансформатора понимается режим его работы при разомкнутой вторичной обмотке. Первичная обмотка трансформатора подключена к источнику переменного напряжения. Ток i_1х первичной обмотки создает переменное магнитное поле, намагничивающее сердечник трансформатора. Магнитный поток в трансформаторе разделим на две части: основной магнитный поток Ф, замыкающийся в сердечнике, и поток рассеяния Ф_1S, замыкающийся частично по воздуху. На рис. 8.3 изображен трансформатор, работающий в режиме холостого хода.

Рисунок 8.3. Трансформатор

Здесь: W₁ - число витков первичной обмотки; W₂ - число витков вторичной обмотки; R₁ - активное сопротивление первичной обмотки.

Определим ЭДС, индуктированную в первичной обмотке трансформатора основным магнитным потоком:

(8.1)

Основной магнитный поток изменяется по синусоидальному закону:

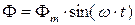(8.2)

где Ф_m - максимальное или амплитудное значение основного магнитного потока; ω = 2πf - угловая частота; f - частота переменного напряжения.

Мгновенное значение ЭДС:

(8.3)

Амплитуда (максимальное значение) ЭДС:

(8.4)

Действующее значение ЭДС в первичной обмотке:

(8.5)

Для действующего значения ЭДС во вторичной обмотке можно получить аналогичную формулу:

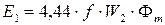(8.6)

Электродвижущие силы E1 и E2, индуцированные в обмотках трансформатора основным магнитным потоком, называются трансформаторными ЭДС. Трансформаторные ЭДС отстают по фазе от основного магнитного потока на 90°.

Магнитный поток рассеяния индуктирует в первичной обмотке ЭДС рассеяния:

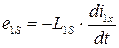(8.7)

где L_1s - индуктивность рассеяния в первичной обмотке.

Запишем уравнение по второму закону Кирхгофа для первичной обмотки:

(8.8)

отсюда:

(8.9)

Выражения для напряжения на первичной катушке имеет три слагаемых: падение напряжения, напряжение, уравновешивающее трансформаторную ЭДС, напряжение, уравновешивающее ЭДС рассеяния.

Запишем уравнение (8.9) в комплексной форме

(8.10)

где 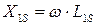индуктивное сопротивление рассеяния первичной обмотки

На рис. 8.2 изображена векторная диаграмма трансформатора, работающего в режиме холостого хода.

Рисунок 8.2. Векторная диаграмма трансформатора, работающего в режиме холостого хода

Векторы трансформаторных ЭДС и 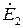отстают на 90° от вектора основного магнитного потока 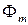. Вектор напряжения параллелен вектору тока , а вектор 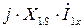опережает вектор тока на 90°. Вектор напряжения на зажимах первичной обмотки трансформатора равен геометрической сумме векторов .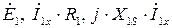

На рис. 8.3 изображена схема замещения трансформатора, соответствующая уравнению (8.10).

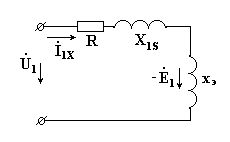
Рисунок 8.3. Схема замещения трансформатора

Здесь X_Э - индуктивное сопротивление, пропорциональное реактивной мощности, затрачиваемой на создание основного магнитного потока.

В режиме холостого хода: (8.11)

Коэффициент трансформации:

Коэффициент трансформации экспериментально определяется из опыта холостого хода.

Глава 9. Механическое действие магнитного поля на проводник с током. Силовая характеристика магнитного поля. Закон Ампера.

На рис. 9.1 показана рамка с током I, находящаяся в однородном магнитном поле B.

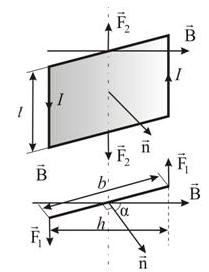
Рисунок 9.1. Рамка с током I, находящаяся в однородном магнитном поле B

Здесь α – угол между нормалью к рамке и вектором магнитной индукции 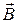(направление нормали связано с направлением тока «правилом буравчика»). Сила Ампера, действующая на сторону рамки длиной l, равна, согласно закону Ампера:

(9.1)

здесь

На другую сторону длиной l действует такая же сила. Получается «пара сил», или вращающий момент:

(9.2)

где плечо Так как – площадь рамки, можно записать

(9.3)

где M – вращающий момент силы, – магнитный момент.

Под действием этого вращающего момента рамка повернётся так, что (рис. 9.2).

Рисунок 9.2. Силы, действующие на рамку с током.

На стороны длиной b тоже действует сила Ампера – растягивая рамку. Так как силы равны по величине и противоположны по направлению, рамка не смещается, в этом случае M =0, состояние устойчивого равновесия.

Когда и 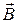антипараллельны (), то снова M =0 (так как плечо равно нулю). Это состояние неустойчивого равновесия. Рамка сжимается и, если чуть сместится, сразу возникает вращающий момент, возвращающий рамку в состояние устойчивого равновесия: .

В неоднородном поле рамка повернется, и будет вытягиваться в область более сильного поля.

Глава 10. Трехфазные цепи. Трехфазные системы, соединенные треугольником. Трехфазная система, соединенная звездой.

Трехфазная цепь является совокупностью трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе на 120º, создаваемые общим источником. Участок трехфазной системы, по которому протекает одинаковый ток, называется фазой.

Трехфазная цепь состоит из трехфазного генератора, соединительных проводов и приемников или нагрузки, которые могут быть однофазными или трехфазными.

Трехфазный генератор представляет собой синхронную машину. На статоре генератора размещена обмотка, состоящая из трех частей или фаз, пространственно смещенных относительно друг друга на 120º. В фазах генератора индуктируется симметричная трехфазная система ЭДС, в которой электродвижущие силы одинаковы по амплитуде и различаются по фазе на 120º. На схемах трехфазных цепей начала фаз обозначают первыми буквами латинского алфавита (А, В, С), а концы - последними буквами (X, Y, Z). Направления ЭДС указывают от конца фазы обмотки генератора к ее началу.. Запишем мгновенные значения и комплексные амплитуды значений ЭДС:

Мгновенные значения:

Соответствующие комплексные амплитуды:

Сумма электродвижущих сил симметричной (амплитуды ЭДС во всех фазах одинаковы, фазы всех ЭДС постоянны) трехфазной системы в любой момент времени равна нулю:

соответственно:

Каждая фаза нагрузки соединяется с фазой генератора двумя проводами: прямым и обратным. Получается несвязанная трехфазная система, в которой имеется шесть соединительных проводов. Чтобы уменьшить количество соединительных проводов, используют трехфазные цепи, соединенные звездой или треугольником.

Соединение звездой.

Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным. Трехфазная цепь, соединенная звездой, изображена на рис. 10.1.

Рисунок 10.1. Трехфазная цепь

Здесь 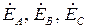- комплексные ЭДС обмоток генератора, - комплексные линейные токи, Za, Zb, Zc - сопротивления соответствующих фазных нагрузок

Провода, идущие от источника к нагрузке называют линейными проводами, провод, соединяющий нейтральные точки источника N и приемника N' называют нейтральным (нулевым) проводом.

Напряжения между началами фаз или между линейными проводами называют линейными напряжениями. Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями.

Токи в фазах приемника или источника называют фазными токами, токи в линейных проводах - линейными токами. Так как линейные провода соединены последовательно с фазами источника и приемника, линейные токи при соединении звездой являются одновременно фазными токами:

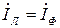(10.1)

Линейные напряжения равны геометрическим разностям соответствующих фазных напряжений

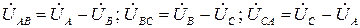(10.2)

На рис. 10.2 изображена векторная диаграмма фазных и линейных напряжений трехфазной цепи, соединенной звездой при симметричной нагрузке. Нагрузка является симметричной, если сопротивления фаз одинаковы.

Рисунок 10.2. Векторная диаграмма фазных и линейных напряжений трехфазной цепи, соединенной звездой при симметричной нагрузке

Из векторной диаграммы видно, что

(10.3)

при соединении звездой линейное напряжение больше фазного в √3 раз.

Соединение в треугольник.

Если конец каждой фазы обмотки генератора соединить с началом следующей фазы, образуется соединение в треугольник. К точкам соединений обмоток подключают три линейных провода, ведущие к нагрузке. На рис. 10.3 изображена трехфазная цепь, соединенная треугольником.

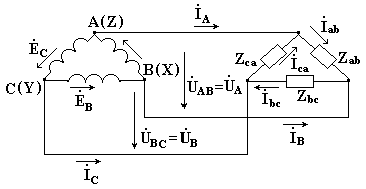
Рисунок 10.3. Трехфазная цепь, соединенная треугольником

Здесь - линейные токи, - фазные токи.

Как видно из рис. 10.3, в трехфазной цепи, соединенной треугольником, фазные и линейные напряжения одинаковы.

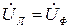(10.4)

Линейные и фазные токи нагрузки связаны между собой первым законом Кирхгофа для узлов а, b, с:

(10.5)

Линейный ток равен геометрической разности соответствующих фазных токов.

На рис. 10.4 изображена векторная диаграмма трехфазной цепи, соединенной треугольником при симметричной нагрузке. Нагрузка является симметричной, если сопротивления фаз одинаковы. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений, так как нагрузка состоит из активных сопротивлений.

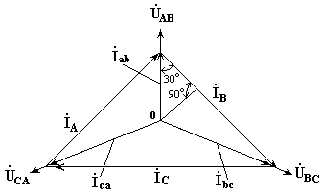
Рисунок 10.4. Векторная диаграмма трехфазной цепи, соединенной треугольником при симметричной нагрузке

Из векторной диаграммы видно, что:

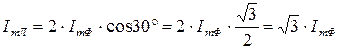(10.6)

При соединении звездой линейный ток в 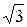раз больше фазного.

Трехфазные цепи, соединенные звездой, получили большее распространение, чем трехфазные цепи, соединенные треугольником. Это объясняется тем, что, во-первых, в цепи, соединенной звездой, можно получить два напряжения: линейное и фазное. Во-вторых, если фазы обмотки электрической машины, соединенной треугольником, находятся в неодинаковых условиях, в обмотке появляются дополнительные токи, нагружающие ее. Такие токи отсутствуют в фазах электрической машины, соединенных по схеме "звезда". Поэтому на практике избегают соединять обмотки трехфазных электрических машин в треугольник.

Мощность в трехфазных цепях.

Трехфазная цепь является обычной цепью синусоидального тока с несколькими источниками. Активная мощность трехфазной цепи равна сумме активных мощностей фаз (используются действующие значения тока и напряжения):

(10.7)

здесь 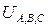- действующие значения фазных напряжений, - действующие значения фазных токов, 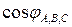- коэффициенты мощности нагрузок, присоединенных к соответствующим фазам.

Формула (10.7) используется для расчета активной мощности в трехфазной цепи при несимметричной нагрузке.

При симметричной нагрузке:

(10.8)

При соединении в треугольник симметричной нагрузки:

(10.9)

При соединении в звезду:

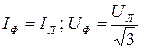(10.10)

В обоих случаях:

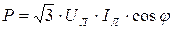(10.11)

В приведенных выше формулах используются действующие значения тока и напряжения.

Глава 11. Электродвигатели постоянного тока. Основные характеристики. Выбор типа электродвигателя.

Электрическая машина постоянного тока состоит из двух основных частей: неподвижной части (индуктора) и вращающейся части (якоря с барабанной обмоткой). На рис. 11.1 изображена конструктивная схема машины постоянного тока

Рисунок 11.1. Конструктивная схема машины постоянного тока

Индуктор состоит из станины 1 цилиндрической формы, изготовленной из ферромагнитного материала, и полюсов с обмоткой возбуждения 2, закрепленных на станине. Обмотка возбуждения создает основной магнитный поток. Магнитный поток может создаваться постоянными магнитами, укрепленными на станине. Якорь состоит из следующих элементов: сердечника 3, обмотки 4, уложенной в пазы сердечника, коллектора 5. Сердечник якоря для уменьшения потерь на вихревые точки набирается из изолированных друг от друга листов электротехнической стали.

Рассмотрим работу машины постоянного тока на модели рис.11.1.

Рисунок 11.1. Модель машины постоянного тока

Здесь 1 - полюсы индуктора, 2 - якорь, 3 - проводники, 4 - контактные щетки. Проводники якорной обмотки расположены на поверхности якоря. Очистим внешние поверхности проводников от изоляции и наложим на проводники неподвижные контактные щетки. Контактные щетки размещены на линии геометрической нейтрали, проведенной посредине между полюсами. Приведем якорь машины во вращение в направлении, указанном стрелкой. Определим направление ЭДС, индуктированных в проводниках якорной обмотки по правилу правой руки. На рис.11. крестиком обозначены ЭДС, направленные от нас, точками - ЭДС, направленные к нам. Соединим проводники между собой так, чтобы ЭДС в них складывались. Для этого соединяют последовательно конец проводника, расположенного в зоне одного полюса с концом проводника, расположенного в зоне полюса противоположной полярности (рис. 11.3).

Рисунок 11.3. Соединения обмоток в машине постоянного тока

Два проводника, соединенные последовательно, образуют один виток или одну катушку. ЭДС проводников, расположенных в зоне одного полюса, различны по величине. Наибольшая ЭДС индуктируется в проводнике, расположенном под срединой полюса, ЭДС, равная нулю, - в проводнике, расположенном на линии геометрической нейтрали. Если соединить все проводники обмотки по о последовательно, то результирующая (суммарная) ЭДС якорной обмотки равна нулю, ток в обмотке отсутствует. Контактные щетки делят якорную обмотку на две параллельные ветви. В верхней параллельной ветви индуктируется ЭДС одного направления, в нижней параллельной ветви - противоположного направления. ЭДС, снимаемая контактными щетками, равна сумме электродвижущих сил проводников, расположенных между щетками. На рис. 11.4 представлена схема замещения якорной обмотки.

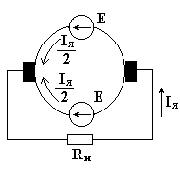
Рисунок11.4. Схема замещения якорной обмотки

В параллельных ветвях действуют одинаковые ЭДС, направленные встречно друг другу. При подключении к якорной обмотке сопротивления в параллельных ветвях возникают одинаковые токи , через сопротивление протекает ток .

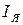ЭДС якорной обмотки E пропорциональна частоте вращения якоря n₂ и магнитному потоку индуктора Ф:

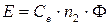(11.1)

где C_e - константа.

В реальных электрических машинах постоянного тока используется специальное контактное устройство - коллектор. Коллектор устанавливается на одном валу с сердечником якоря и состоит из отдельных изолированных друг от друга и от вала якоря медных пластин. Каждая из пластин соединена с одним или несколькими проводниками якорной обмотки. На коллектор накладываются неподвижные контактные щетки. С помощью контактных щеток вращающаяся якорная обмотка соединяется с сетью постоянного тока или с нагрузкой.

Работа электрической машины постоянного тока в режиме генератора.

Любая электрическая машина обладает свойством обратимости, т.е. может работать в режиме генератора или двигателя. Если к зажимам приведенного во вращение якоря генератора присоединить сопротивление нагрузки, то под действием ЭДС якорной обмотки E в цепи возникает ток. Уравнение по второму закону Кирхгофа для этого случая:

(11.2)

где U - напряжение на зажимах генератора; R_я - сопротивление обмотки якоря. Отсюда:

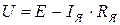(11.3)

Уравнение (11.3) называется основным уравнением генератора. С появлением тока в проводниках обмотки возникнут электромагнитные силы.

На рис. 11.5 схематично изображен генератор постоянного тока, показаны направления токов в проводниках якорной обмотки.

Рисунок 11.5. Генератор постоянного тока

Воспользовавшись правилом левой руки, видим, что электромагнитные силы создают электромагнитный момент М_эм, препятствующий вращению якоря генератора. Чтобы машина работала в качестве генератора, необходимо первичным двигателем вращать ее якорь, преодолевая тормозной электромагнитный момент.

Магнитное поле генератора с независимым возбуждением создается током, подаваемым от постороннего источника энергии в обмотку возбуждения полюсов. Схема генератора с независимым возбуждением показана на рис. 11.6. Магнитное поле генераторов с независимым возбуждением может создаваться от постоянных магнитов (рис. 11.7).

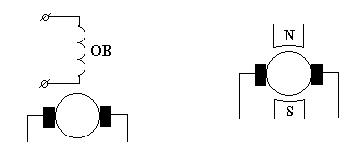
рис 11.6 рис. 11.7

Зависимость ЭДС генератора от тока возбуждения называется характеристикой холостого хода E = U_хх = f (I_в). Характеристику холостого хода получают при разомкнутой внешней цепи и при постоянной частоте вращения (n₂ = const)

Характеристика холостого хода генератора показана на рис. 11.8.

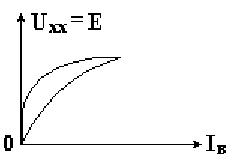
Рисунок 11.8. Характеристика холостого хода генератора

Из-за остаточного магнитного потока ЭДС генератора не равна нулю при токе возбуждения, равном нулю. При увеличении тока возбуждения ЭДС генератора сначала возрастает пропорционально току возбуждения. Соответствующая часть характеристики холостого хода будет прямолинейна. Но при дальнейшем увеличении тока возбуждения происходит магнитное насыщение машины, отчего кривая будет иметь изгиб. При последующем возрастании тока возбуждения ЭДС генератора почти не меняется. Если уменьшать ток возбуждения, кривая размагничивания не совпадает с кривой намагничивания из-за явления гистерезиса.

Зависимость напряжения на внешних зажимах машины от величины тока нагрузки U = f (I) при токе возбуждения I_в = const называют внешней характеристикой генератора. Внешняя характеристика генератора изображена на рис. 11.9.

Рисунок 11.9. Внешняя характеристика генератора

С ростом тока нагрузки напряжение на зажимах генератора уменьшается из-за увеличения падения напряжения в якорной обмотке.

Недостатком генератора с независимым возбуждением является необходимость иметь отдельный источник питания. Но при определенных условиях обмотку возбуждения можно питать током якоря генератора.

Самовозбуждающиеся генераторы имеют одну из трех схем: с параллельным, последовательным и смешанным возбуждением. На рис. 11.10 изображен генератор с параллельным возбуждением.

Рисунок 11.10. Генератор с параллельным возбуждением.

Обмотка возбуждения подключена параллельно якорной обмотке. В цепь возбуждения включен реостат Rв. Генератор работает в режиме холостого хода. Чтобы генератор самовозбудился, необходимо выполнение определенных условий.

Первым из этих условий является наличие остаточного магнитного потока между полюсами. При вращении якоря остаточный магнитный поток индуцирует в якорной обмотке небольшую остаточную ЭДС.

Вторым условием является согласное включение обмотки возбуждения. Обмотки возбуждения и якоря должны быть соединены таким образом, чтобы ЭДС якоря создавала ток, усиливающий остаточный магнитный поток. Усиление магнитного потока приведет к увеличению ЭДС. Машина самовозбуждается и начинает устойчиво работать с каким-то током возбуждения I_в = const и ЭДС Е = const, зависящими от сопротивления R_в в цепи возбуждения.

Третьим условием является то, что сопротивление цепи возбуждения при данной частоте вращения должно быть меньше критического. Изобразим на рис. 11.11 характеристику холостого хода генератора E = f (Iв) (кривая 1) и вольт - амперную характеристику сопротивления цепи возбуждения Uв = Rв·Iв, где Uв - падение напряжения в цепи возбуждения. Эта характеристика представляет собой прямую линию 2, наклоненную к оси абсцисс под углом γ (tg γ ~ Rв).

Рисунок 11.11. Характеристики генератора

Ток обмотки возбуждения увеличивает магнитный поток полюсов при согласном включении обмотки возбуждения. ЭДС, индуцированная в якоре, возрастает, что приводит к дальнейшему увеличению тока обмотки возбуждения, магнитного потока и ЭДС. Рост ЭДС от тока возбуждения замедляется при насыщении магнитной цепи машины.

Падение напряжения в цепи возбуждения пропорционально росту тока. В точке пересечения характеристики холостого хода машины 1 с прямой 2 процесс самовозбуждения заканчивается. Машина работает в устойчивом режиме.

Если увеличим сопротивление цепи обмотки возбуждения, угол наклона прямой 2 к оси тока возрастает. Точка пересечения прямой с характеристикой холостого хода смещается к началу координат. При некотором значении сопротивления цепи возбуждения Rкр, когда

γ = γкр, самовозбуждение становится невозможным. При критическом сопротивлении вольт - амперная характеристика цепи возбуждения становится касательной к прямолинейной части характеристики холостого хода, а в якоре появляется небольшая ЭДС.

Работа электрической машины постоянного тока в режиме двигателя.

Под действием напряжения, подведенного к якорю двигателя, в обмотке якоря появится ток I_я. При взаимодействии тока с магнитным полем индуктора возникает электромагнитный вращающий момент

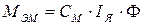(11.5)

где C_М - коэффициент, зависящий от конструкции двигателя.

На рис. 11.12 изображен схематично двигатель постоянного тока, выделен проводник якорной обмотки.

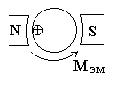
Рисунок 11.12. Двигатель постоянного тока

Ток в проводнике направлен от нас. Направление электромагнитного вращающего момента определится по правилу левой руки. Якорь вращается против часовой стрелки. В проводниках якорной обмотки индуцируется ЭДС, направление которой определяется правилом правой руки. Эта ЭДС направлена встречно току якоря, ее называют противо-ЭДС.

В установившемся режиме электромагнитный вращающий момент М_эм уравновешивается противодействующим тормозным моментом М₂ механизма, приводимого во вращение (). На рис. 11.13 показана схема замещения якорной обмотки двигателя. ЭДС направлена встречно току якоря.

Рисунок 11.13. Схема замещения якорной обмотки двигателя

В соответствии со вторым законом Кирхгофа: , откуда:

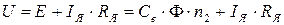(11.6)

Это выражение называется основным уравнением двигателя. Из уравнения 12.6 можно получить следующие формулы:

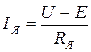(11.7)

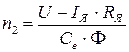(11.8)

Магнитный поток Ф зависит от тока возбуждения I_в, создаваемого в обмотке возбуждения. Из формулы (11.8) видно, что частоту вращения двигателя постоянного тока n₂ можно регулировать следующими способами:

1. изменением тока возбуждения с помощью реостата в цепи обмотки возбуждения;
2. изменением тока возбуждения с помощью реостата в цепи обмотки возбуждения;
3. изменением напряжения U на зажимах якорной обмотки.

Чтобы изменить направление вращения двигателя на обратное (реверсировать двигатель), необходимо изменить направление тока в обмотке якоря или индуктора.

Механические характеристики электродвигателей постоянного тока

Рассмотрим двигатель с параллельным возбуждением в установившемся режиме работы (рис. 11.14). Обмотка возбуждения подключена параллельно якорной обмотке.

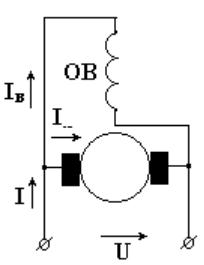
Рисунок 11.14. Двигатель с параллельным возбуждением

, отсюда:

(11.9)

тогда с учетом 11.7 и 11.8:

(11.10)

Механической характеристикой двигателя называется зависимость частоты вращения якоря n₂ от момента на валу M₂ при U = const и I_в = const.Уравнение (11.10) является уравнением механической характеристики двигателя с параллельным возбуждением. Эта характеристика является жесткой. С увеличением нагрузки частота вращения такого двигателя уменьшается в небольшой степени (рис. 11.15)

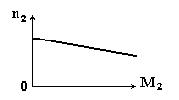
Рисунок 11.15. Механическая характеристика двигателя с параллельным возбуждением

На рисунке 11.16 изображен двигатель последовательного возбуждения. Якорная обмотка и обмотка возбуждения включены последовательно.

Рисунок 11.16. Двигатель последовательного возбуждения

Ток возбуждения двигателя одновременно является током якоря. Магнитный поток индуктора пропорционален току якоря:

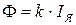(11.11)

где k - коэффициент пропорциональности.

Момент на валу двигателя пропорционален квадрату тока якоря.

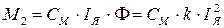(11.12)

откуда:

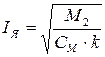(11.13)

Уравнение механической характеристики двигателя последовательного возбуждения выглядит следующим образом:

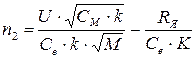(11.14)

Механическая характеристика двигателя последовательного возбуждения является мягкой (рис. 11.17).

Рисунок 11.17. Механическая характеристика двигателя последовательного возбуждения

С увеличением нагрузки скорость двигателя резко падает.

С уменьшением нагрузки на валу двигатель развивает очень большую частоту вращения. Говорят, что двигатель идет вразнос. Работа двигателя последовательного возбуждения без нагрузки недопустима.

Двигатель смешанного возбуждения имеет механическую характеристику, представляющую собой нечто среднее между механическими характеристиками двигателя параллельного и последовательного возбуждения.

Двигатели с параллельным возбуждением применяются для привода станков и различных механизмов, требующих широкой регулировки скорости.

Двигатели с последовательным возбуждением применяются в качестве тяговых двигателей электровозов, трамваев и т.д.

Глава 12. Электродвигатели переменного тока. Устройство и принцип действия асинхронного двигателя. Аппаратура управления. Режим работы электроприводов.

Особенностью многофазных систем является возможность создать в механически неподвижном устройстве вращающееся магнитное поле. Катушка, подключенная к источнику переменного тока, образует пульсирующее магнитное поле, т.е. магнитное поле, изменяющееся по величине и направлению.

Возьмем цилиндр с внутренним диаметром D. На поверхности цилиндра разместим три катушки, пространственно смещенные относительно друг друга на 120º. Катушки подключим к источнику трехфазного напряжения (рис. 12.1).

Рисунок 12.1. Схема включения асинхронного двигателя

На рис. 12.2 показан график изменения мгновенных токов, образующих трехфазную систему.

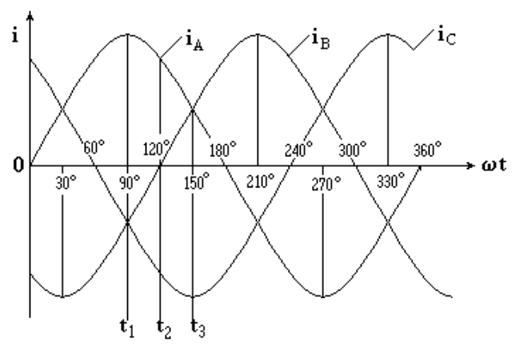
Рисунок 12.2. График изменения мгновенных токов, образующих трехфазную систему

Каждая из катушек создает пульсирующее магнитное поле. Магнитные поля катушек, взаимодействуя друг с другом, образуют результирующее вращающееся магнитное поле, характеризующееся вектором результирующей магнитной индукции .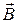

На рис. 12.3 изображены векторы магнитной индукции каждой фазы и результирующий вектор 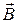построенные для трех моментов времени t1, t2, t3. Положительные направления осей катушек обозначены +1, +2, +3.

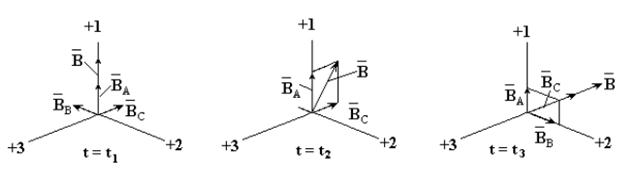
Рисунок 12.3. Векторы магнитной индукции каждой фазы и результирующий вектор 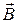построенные для трех моментов времени t1, t2, t3.

В момент t = t1 ток и магнитная индукция в катушке А-Х положительны и максимальны, в катушках В-Y и C-Z - одинаковы и отрицательны. Вектор результирующей магнитной индукции равен геометрической сумме векторов магнитных индукций катушек и совпадает с осью катушки А-Х. В момент t = t2 токи в катушках А-Х и С-Z одинаковы по величине и противоположны по направлению. Ток в фазе В равен нулю. Результирующий вектор магнитной индукции повернулся по часовой стрелке на 30º. В момент t = t3 токи в катушках А-Х и В-Y одинаковы по величине и положительны, ток в фазе C-Z максимален и отрицателен, вектор результирующего магнитного поля размещается в отрицательном направлении оси катушки С-Z. За период переменного тока вектор результирующего магнитного поля повернется на 360º. Линейная скорость перемещения вектора магнитной индукции:

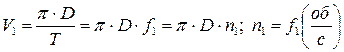(12.1)

где f₁ - частота переменного напряжения; Т - период синусоидального тока; n₁ - частота вращения магнитного поля или синхронная частота вращения.

За период Т магнитное поле перемещается на расстояние 2τ, где 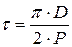- полюсное деление или расстояние между полюсами магнитного поля по длине окружности цилиндра диаметром D, а P - число пар полюсов магнитного поля.

Линейная скорость: (12.2)

Откуда 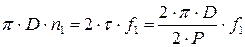и число оборотов в секунду и в минуту:

(12.3)

где n₁ - синхронная частота вращения многополюсного магнитного поля с числом пар полюсов Р. Катушки, изображенные на рис. 12.1, создают двухполюсное магнитное поле, с числом полюсов 2 Р = 2. Частота вращения поля равна 3000 об/мин. Чтобы получить четырехполюсное магнитное поле, необходимо внутри цилиндра диаметром D поместить шесть катушек, по две на каждую фазу. Тогда, согласно формуле (12.3), магнитное поле будет вращаться в два раза медленней, с n₁ = 1500 об/мин.

Чтобы получить вращающееся магнитное поле, необходимо выполнить два условия.

1. Иметь хотя бы две пространственно смещенные катушки.
2. Подключить к катушкам несовпадающие по фазе токи.

Асинхронные двигатели. Конструкция, принцип действия

Асинхронный двигатель имеет неподвижную часть, именуемую статором, и вращающуюся часть, называемую ротором. В статоре размещена обмотка, создающая вращающееся магнитное поле. Различают асинхронные двигатели с короткозамкнутым и фазным ротором. В пазах ротора с короткозамкнутой обмоткой размещены алюминиевые или медные стержни. По торцам стержни замкнуты алюминиевыми или медными кольцами. Статор и ротор набирают из листов электротехнической стали, чтобы уменьшить потери на вихревые токи. Фазный ротор имеет трехфазную обмотку (для трехфазного двигателя). Концы фаз соединены в общий узел, а начала выведены к трем контактным кольцам, размещенным на валу. На кольца накладывают неподвижные контактные щетки. К щеткам подключают пусковой реостат. После пуска двигателя сопротивление пускового реостата плавно уменьшают до нуля.

Принцип действия асинхронного двигателя рассмотрим на модели, представленной на рисунке 12.4.

Рисунок 12.4. Модель асинхронного двигателя

Вращающееся магнитное поле статора представим в виде постоянного магнита, вращающегося с синхронной частотой вращения n₁. В проводниках замкнутой обмотки ротора индуктируются токи. Полюса магнита перемещаются по часовой стрелке. Наблюдателю, разместившемуся на вращающемся магните, кажется, что магнит неподвижен, а проводники роторной обмотки перемещаются против часовой стрелки. Направления роторных токов, определенные по правилу правой руки, указаны на рис. 12.4. Пользуясь правилом левой руки, найдем направление электромагнитных сил, действующих на ротор и заставляющих его вращаться. Ротор двигателя будет вращаться с частотой вращения n₂ в направлении вращения поля статора. Ротор вращается асинхронно т.е частота вращения его n₂ меньше частоты вращения поля статора n₁. Относительная разность скоростей поля статора и ротора называется скольжением:

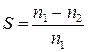(12.4)

Скольжение не может быть равным нулю, так как при одинаковых скоростях поля и ротора прекратилось бы наведение токов в роторе и, следовательно, отсутствовал бы электромагнитный вращающий момент. Вращающий электромагнитный момент уравновешивается противодействующим тормозным моментом М_эм = М₂.

С увеличением нагрузки на валу двигателя тормозной момент становится больше вращающего, и скольжение увеличивается. Вследствие этого, возрастают индуктированные в роторной обмотке ЭДС и токи. Вращающий момент увеличивается и становится равным тормозному моменту. Вращающий момент может возрастать с увеличением скольжения до определенного максимального значения, после чего при дальнейшем увеличении тормозного момента вращающий момент резко уменьшается, и двигатель останавливается.

Скольжение заторможенного двигателя равно единице. Говорят, что двигатель работает в режиме короткого замыкания.

Частота вращения ненагруженного асинхронного двигателя n₂ приблизительно равна синхронной частоте n₁. Скольжение ненагруженного двигателя S» 0. Говорят, что двигатель работает в режиме холостого хода.

Скольжение асинхронной машины, работающей в режиме двигателя, изменяется от нуля до единицы.

Асинхронная машина может работать в режиме генератора. Для этого ее ротор необходимо вращать сторонним двигателем в направлении вращения магнитного поля статора с частотой n₂ > n₁. Скольжение асинхронного генератора:

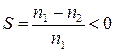(12.5)

Асинхронная машина может работать в режиме электромашинного тормоза. Для этого необходимо ее ротор вращать в направлении, противоположном направлению вращения магнитного поля статора.

В этом режиме S > 1. Как правило, асинхронные машины используются в режиме двигателя. Асинхронный двигатель является наиболее распространенным в промышленности типом двигателя. Частота вращения поля в асинхронном двигателе жестко связана с частотой сети f₁ и числом пар полюсов P статора. При частоте f₁ = 50 Гц существует следующий ряд частот вращения.

P
n1, об/мин	3 000

Из формулы 12.3 получим:

(12.6)

Скорость поля статора относительно ротора называется скоростью скольжения:

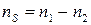(12.7)

Частота тока и ЭДС в роторной обмотке:

(12.8)

Асинхронная машина с заторможенным ротором работает как трансформатор. Основной магнитный поток индуктирует в статорной и в неподвижной роторной обмотках ЭДС Е₁ и Е_2к.:

(12.9)

где Ф_m - максимальное значение основного магнитного потока, сцепленного со статорной и роторной обмотками; W₁ и W₂ - числа витков статорной и роторной обмоток; f₁ - частота напряжения в сети; K₀₁ и K₀₂ - обмоточные коэффициенты статорной и роторной обмоток.

Чтобы получить более благоприятное распределение магнитной индукции в воздушном зазоре между статором и ротором, статорные и роторные обмотки не сосредоточивают в пределах одного полюса, а распределяют по окружностям статора и ротора. ЭДС распределенной обмотки меньше ЭДС сосредоточенной обмотки. Этот факт учитывается введением в формулы, определяющие величины электродвижущих сил обмоток, обмоточных коэффициентов. Величины обмоточных коэффициентов несколько меньше единицы.

ЭДС в обмотке вращающегося ротора:

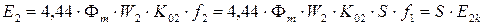(12.10)

Вращающий момент асинхронного двигателя:

На ротор и полюсы статора действуют электромагнитные вращающие моменты, одинаковые по величине и направленные в противоположные стороны. Мощность, необходимая для вращения статорных полюсов с синхронной частотой:

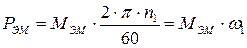(12.11)

где 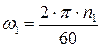- угловая скорость. Механическая мощность, развиваемая ротором:

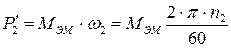(12.12)

где - угловая скорость ротора.

Разность мощностей:

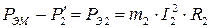(12.13)

где Р_Э2 - электрические потери в роторной обмотке; m₂ - число фаз обмотки ротора; R₂ - активное сопротивление обмотки ротора; I₂ - ток ротора.

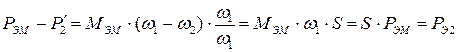(12.14)

Откуда:

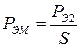(12.15)

Вращающий момент:

(12.16)

На рис. 12.5 изображена зависимость электромагнитного момента от скольжения в виде сплошной линии.

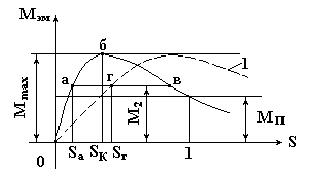
Рисунок 12.5 Нагрузочная характеристика асинхронного двигателя

Пусть исполнительный механизм, приводимый во вращение данным двигателем, создает противодействующий тормозной момент М2. На рис.12.5 имеются две точки, для которых справедливо равенство Мэм = М2; это точки а и в. В точке а двигатель работает устойчиво. Если двигатель под влиянием какой-либо причины уменьшит частоту вращения, то скольжение его возрастет, вместе с ним возрастет вращающий момент. Благодаря этому частота вращения двигателя повысится, и вновь восстановится равновесие Мэм = М2;.В точке в работа двигателя не может быть устойчива: случайное отклонение частоты вращения приведет либо к остановке двигателя, либо к переходу его в точку а. Следовательно, вся восходящая ветвь характеристики является областью устойчивой работы двигателя, а вся нисходящая часть - областью неустойчивой работы. Точка б, соответствующая максимальному моменту, разделяет области устойчивой и неустойчивой работы. Максимальному значению вращающего момента соответствует критическое скольжение S_k. Скольжению S = 1 соответствует пусковой момент. Если величина противодействующего тормозного момента М₂ больше пускового М_П, двигатель при включении не запустится, останется неподвижным.

Значение максимального момента:

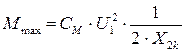(12.17)

где CM - коэффициент,

Можно сделать следующие выводы:

1. величина максимального вращающего момента не зависит от активного сопротивления цепи ротора;
2. с увеличением активного сопротивления цепи ротора максимальный вращающий момент, не изменяясь по величине, смещается в область больших скольжений (см. кривая 1 рис. 12.5);
3. вращающий момент пропорционален квадрату напряжения сети.

Механической характеристикой асинхронного двигателя называется зависимость частоты вращения двигателя от момента на валу n2 = f (M2). Механическую характеристику получают при условии U1 - const, f1 - const. Механическая характеристика двигателя является зависимостью вращающего момента от скольжения, построенной в другом масштабе. На рис. 12.6 изображена типичная механическая характеристика асинхронного двигателя.

Рисунок 12.6. Механическая характеристика асинхронного двигателя

С увеличением нагрузки величина момента на валу возрастает до некоторого максимального значения, а частота вращения уменьшается. Как правило, у асинхронного двигателя пусковой момент меньше максимального. Это объясняется тем, что в пусковом режиме, когда n2 = 0, а S = 1 асинхронный двигатель находится в режиме, аналогичном короткому замыканию в трансформаторе. Магнитное поле ротора направлено встречно магнитному полю статора.

Регулирование частоты вращения асинхронных двигателей. Реверсирование асинхронного двигателя.

Частоты вращения ротора и магнитного поля связаны соотношением:

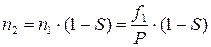(12.18)

Из формулы (12.18) видно, что частоту вращения асинхронного двигателя можно менять тремя способами:

1. изменением частоты питающего напряжения;
2. изменением числа полюсов двигателя. Для этого в пазы статора закладывают обмотку, которую можно переключать на различное число полюсов;
3. изменением скольжения. Этот способ можно применить в асинхронных двигателях с фазным ротором. Для этого в цепь ротора включают регулировочный реостат. Увеличение активного сопротивления цепи ротора приводит к увеличению скольжения от S_a к S_г (см. рис. 12.5), а, следовательно, и к уменьшению частоты вращения двигателя.

Асинхронные двигатели имеют простую конструкцию и надежны в эксплуатации. Недостатком асинхронных двигателей является трудность регулирования их частоты вращения.

Чтобы реверсировать трехфазный асинхронный двигатель (изменить направление вращения двигателя на противоположное), необходимо поменять местами две фазы, то есть поменять местами два любых линейных провода, подходящих к обмотке статора двигателя. Однофазные асинхронные двигатели.

Однофазный двигатель имеет одну обмотку, расположенную на статоре. Однофазная обмотка, питаемая переменным током, создаст переменное магнитное поле. Поместим в это поле ротор с короткозамкнутой обмоткой. Ротор вращаться не будет. Если раскрутить ротор сторонней механической силой в любую сторону, двигатель будет устойчиво работать. Объяснить это можно следующим образом. Переменное магнитное поле можно заменить двумя магнитными полями, вращающимися в противоположных направлениях с синхронной частотой n₁ и имеющими амплитуды магнитных потоков, равные половине амплитуды магнитного потока пульсирующего поля. Одно из магнитных полей называется прямовращающимся, другое - обратновращающимся. Каждое из магнитных полей индуктирует в роторной обмотке вихревые токи. При взаимодействии вихревых токов с магнитными полями образуются вращающие моменты, направленные встречно друг другу.

На рис. 12.7 изображены зависимости момента от прямого поля М', момента от

обратного поля М" и результирующего момента М в функции скольжения М = М' - M".

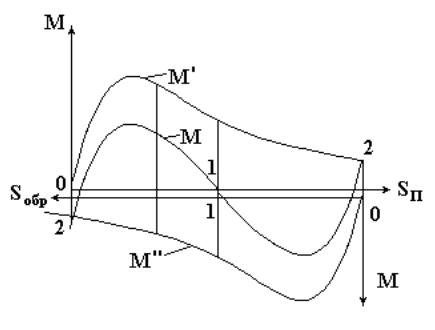
Рисунок 12.7. Зависимости моментов двигателя от коэффициента скольжения.

В пусковом режиме на ротор действуют вращающие моменты, одинаковые по величине и противоположные по направлению. Раскрутим ротор сторонней силой в направлении прямовращающегося магнитного поля. Появится избыточный (результирующий) вращающий момент, разгоняющий ротор до скорости, близкой к синхронной. При этом скольжение двигателя относительно прямовращающегося магнитного поля

(12.19)

Скольжение двигателя относительно обратновращающегося магнитного поля:

(12.20)

Рассматривая результирующую характеристику, можно сделать следующие выводы:

1. Однофазный двигатель не имеет пускового момента. Он будет вращаться в ту сторону, в которую раскручен внешней силой.
2. Из-за тормозного действия обратновращающегося поля характеристики однофазного двигателя хуже, чем трехфазного.

Для создания пускового момента однофазные двигатели снабжают пусковой обмоткой, пространственно смещенной относительно основной, рабочей обмотки на 90º. Пусковая обмотка подключается к сети через фазосдвигающие элементы: конденсатор или активное сопротивление.

На рис. 12.8 показана схема включения обмоток двигателя, где Р - рабочая обмотка, П - пусковая обмотка. Емкость фазосдвигающего элемента С подбирают таким образом, чтобы токи в рабочей и пусковой обмотках различались по фазе на 90º.

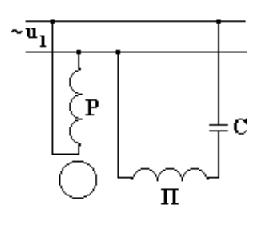
Рисунок 12.8. Схема включения обмоток однофазного двигателя

Трехфазный асинхронный двигатель может работать от однофазной сети, если подключить его обмотки по следующим схемам.(рис. 12.9)

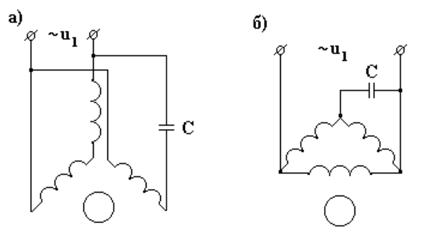
Рисунок 12.9. Схема включения обмоток асинхронного двигателя при питании от однофазной сети

В схеме на рис. 12.9а статорные обмотки соединены звездой. В схеме на рис. 12.9б статорные обмотки соединены треугольником. Величина емкости С ≈ 60 мкФ на 1 кВт мощности

Синхронные двигатели.

В отличие от асинхронного двигателя частота вращения синхронного двигателя постоянная при различных нагрузках. Синхронные двигатели находят применение для привода машин постоянной скорости (насосы, компресоры, вентиляторы).

В статоре синхронного электродвигателя размещается обмотка, подключаемая к сети трехфазного тока и образующая вращающееся магнитное поле. Ротор двигателя состоит из сердечника с обмоткой возбуждения. Обмотка возбуждения через контактные кольца подключается к источнику постоянного тока. Ток обмотки возбуждения создает магнитное поле, намагничивающее ротор.

Роторы синхронных машин могут быть явнополюсными (с явновыраженными полюсами) и неявнополюсными (с неявновыраженными полюсами). На рис. 12.10а изображен сердечник 1 явнополюсного ротора с выступающими полюсами. На полюсах размещены катушки возбуждения 2. На рисунке 12.10б изображен неявнополюсной ротор, представляющий собой ферромагнитный цилиндр 1. На поверхности ротора в осевом направлении фрезеруют пазы, в которые укладывают обмотку возбуждения 2.

Рисунок 12.10. Неявнополюсной ротор

Рассмотрим принцип работы синхронного двигателя на модели (рис. 12.11).

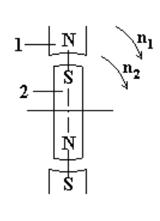
Рисунок 12.11. Модель неявнополюсного ротора

Вращающееся магнитное поле статора представим в виде магнита 1. Намагниченный ротор изобразим в виде магнита 2. Повернем магнит 1 на угол α. Северный магнитный полюс магнита 1 притянет южный полюс магнита 2, а южный полюс магнита 1 - северный полюс магнита 2. Магнит 2 повернется на такой же угол α. Будем вращать магнит 1. Магнит 2 будет вращаться вместе с магнитом 1, причем частоты вращения обоих магнитов будут одинаковыми, синхронными, n₂ = n₁.

Синхронный двигатель, на роторе которого отсутствует обмотка возбуждения, называется синхронным реактивным двигателем. Ротор синхронного реактивного двигателя изготавливается из ферромагнитного материала и должен иметь явновыраженные полюсы. Вращающееся магнитное поле статора намагничивает ротор. Явнополюсный ротор имеет неодинаковые магнитные сопротивления по продольной и поперечной осям полюса. Силовые линии магнитного поля статора изгибаются, стремясь пройти по пути с меньшим магнитным сопротивлением. Деформация магнитного поля вызовет, вследствие упругих свойств силовых линий, реактивный момент, вращающий ротор синхронно с полем статора. Если к вращающемуся ротору приложить тормозной момент, ось магнитного поля ротора повернется на угол θ относительно оси магнитного поля статора. С увеличением нагрузки этот угол возрастает. Если нагрузка превысит некоторое допустимое значение, двигатель остановится, выпадет из синхронизма.

У синхронных двигателей отсутствует пусковой момент. Это объясняется тем, что электромагнитный вращающий момент, воздействующий на неподвижный ротор, меняет свое направление два раза за период Т переменного тока. Из-за своей инерционности, ротор не успевает тронуться с места и развить необходимое число оборотов.

В настоящее время применяется асинхронный пуск синхронного двигателя. В пазах полюсов ротора укладывается дополнительная короткозамкнутая обмотка.

Вращающее магнитное поле статора индуктирует в короткозамкнутой пусковой обмотке вихревые токи. При взаимодействии этих токов с магнитным полем статора образуется асинхронный электромагнитный момент, приводящий ротор во вращение. Когда частота вращения ротора приближается к частоте вращения статорного поля, двигатель втягивается в синхронизм и вращается с синхронной скоростью. Короткозамкнутая обмотка не перемещается относительно поля, вихревые токи в ней не индуктируются, асинхронный пусковой момент становится равным нулю.

Глава 13. Полупроводниковые приборы. Выпрямительные устройства. Типы выпрямителей. Основные параметры. Сглаживающие фильтры. Коэффициент пульсации. Коэффициент сглаживания.

Полупроводники – материалы, обладающие средней проводимостью между хорошими проводниками и хорошими диэлектриками. Особенностью полупроводников является уменьшение сопротивления с ростом температуры. В качестве полупроводников наиболее часто используют германий (Ge), кремний (Si), арсенид галлия, селен, различные оксиды, нитриды и карбиды. Поведение атома определяется валентными электронами. Любое свойство можно представить соответствующими энергетическими диаграммами, на которых изображаются валентная зона, зона проводимости и запрещенная зона (рисунок 13.1).

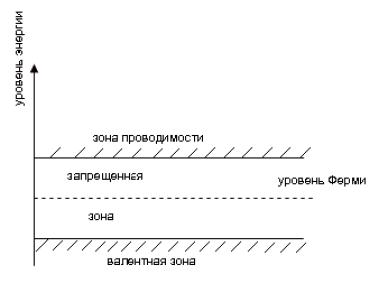
Рисунок 13.1. Зонная диаграмма полупроводника

Валентная зона представляет совокупность разрешённых энергий для валентных электронов. Зона проводимости – совокупность разрешенных энергий для свободных электронов. Именно свободные электроны способны создать ток под действием приложенного внешнего напряжения или под действием разности концентраций (градиента) носителей заряда. Запрещенная зона - совокупность энергий, которые запрещены для электронов данного вещества. В запрещённой зоне нет энергетических уровней (если они не созданы специально, например, атомами примесей), на которых могли бы находиться электроны. Ширина запрещённой зоны у используемых в настоящее время в качестве полупроводников материалов лежит в диапазоне от 0,1эВ до 3эВ (электронвольт).

В запрещенной зоне можно определить для полупроводников уровень Ферми. Уровень Ферми это энергетический уровень, вероятность появления электрона на котором равна 1/2. Для полупроводника положение уровня Ферми определяется концентрацией носителей заряда. Если использовать вероятностную функцию Ферми, то можно заметить, что при температуре близкой к нулю полупроводник превращается в хороший диэлектрик. С ростом температуры увеличивается вероятность попадания электронов в зону проводимости и появляется электропроводность у полупроводников.

Известно, что в полупроводниках Ge, Si имеется по четыре валентных электрона, которые при сближении атомов в составе вещества образуют новые, ковалентные связи. Это приводит к тому, что совокупная энергия системы оказывается минимальной и система оказывается устойчивой. При разрушении ковалентной связи электрон оказывается в зоне проводимости и образует свободный носитель заряда. Нарушенная ковалентная связь называется «дыркой», она ведет себя подобно положительному заряду. В результате разрушения ковалентной связи генерируется пара электрон-дырка, процесс зарождения свободных носителей заряда называется генерацией.

Процесс генерации в полупроводниках может происходить под действием температуры, света, электрического поля (ударной ионизации) и под действием какого-либо излучения.

Обратный процесс называется рекомбинацией, когда свободный электрон восстанавливает ковалентную связь. Чтобы повысить быстродействие полупроводниковых приборов для обеспечения меньшего времени рекомбинации используют специальные центры рекомбинации – примеси, разрешённые энергетические уровни которых располагаются в запрещённой зоне исходного полупроводника.

Собственный полупроводник – абсолютно чистый и однородный полупроводник, у которого количество свободных электронов равно количеству дырок. Энергия Ферми в собственном полупроводнике располагается посередине запрещенной зоны. Если в полупроводниковом приборе используется собственный полупроводник, то это подчеркивается в описании этого прибора символом «i». Концентрация свободных электронов в собственном полупроводнике обозначается символом n_i, а свободных дырок – символом p_i.

Примесный полупроводник.

Полупроводник n-типа или электронный полупроводник образуется из собственного полупроводника путём добавления пятивалентных атомов мышьяка, сурьмы, фосфора (Рис. 13.2).

Рисунок 13.2. Электронный полупроводник

В этом случае пятый валентный электрон не участвует в образовании ковалентной связи, уровень энергии этого электрона оказывается близок к энергии дна зоны проводимости. То есть, чтобы этот электрон освободился достаточно небольшого приращения энергии. Значительное количество атомов в примеси приводит к повышению энергии Ферми в сторону зоны проводимости.

Концентрация свободных электронов в электронном полупроводнике обозначается символом n_n. Одновременно со свободными электронами в n-полупроводнике имеются свободные дырки, концентрация которых обозначается символом p_n. Дырки в электронном полупроводнике являются неосновными носителями заряда.

Полупроводник p-типа или дырочный полупроводник, обладающий дырочной проводимостью, образуется добавлением трехвалентных атомов алюминия, бора, индия или галлия (рис. 13.3).

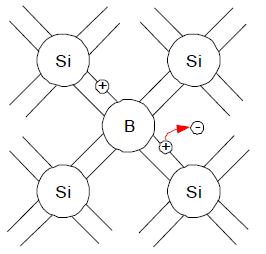
Рисунок 13.3. Дырочный полупроводник

При этом при образовании ковалентных связей одна связь окажется недостроенной и какой-либо электрон, разрушая существующую ковалентную связь, достраивает данную связь, образуя неподвижный ион. Разрушенная ковалентная связь соответствует дырке. При этом уровень энергии Ферми смещается вниз относительно середины запрещённой зоны.

Концентрация свободных дырок в дырочном полупроводнике обозначается символом p_p. Одновременно со свободными дырками в p-полупроводнике имеются свободные электроны, концентрация которых обозначается символом n_p. Электроны в дырочном полупроводнике являются неосновными носителями заряда.

Для любого полупроводника справедливо равенство:

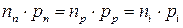(13.1)

Токи в полупроводниках

Различают четыре разновидности токов в зависимости от типа свободных носителей заряда и от причины их движения:

− дырочный

− электронный

− диффузионный

− дрейфовый.

Дырочный ток – направленное движение дырок под действием какой-либо причины, а электронный ток – направленное движение электронов. Причиной появления тока может быть внешнее электрическое поле, приложенное к полупроводнику (дрейфовый ток) или различие в концентрациях носителей заряда (диффузионный ток).

Сочетая причину тока и тип свободных носителей заряда, образующих ток в данном случае, можно выделить следующие четыре разновидности токов в полупроводниках:

• дрейфовый электронный ток

• дрейфовый дырочный ток

• диффузионный электронный ток

• диффузионный дырочный ток.

Величина электронного и дырочного токов зависит от подвижности электронов или дырок. Если напряженность внешнего электрического поля повышается, то пропорционально будет расти скорость носителей зарядов и ток. Но при достижении определенной критической скорости дальнейший рост скорости носителей заряда прекращается.

Дата добавления: 2014-01-06