Энергетический баланс в электрических цепях

Составление уравнений для расчета токов в схемах при помощи законов Кирхгофа

Законы Кирхгофа используются для нахождения токов в ветвях схемы. Так как в каждой ветви схемы протекает свой ток, то число неизвестных токов равняется числу ветвей схем. Перед тем как составлять уравнения, необходимо:

1. Произвольно выбрать положительные направления токов в ветвях и обозначить их на схеме.

2. Выбрать положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа.

Для единообразия рекомендуется положительные направления обхода контуров выбрать одинаковыми для всех контуров, например, по часовой стрелке.

Обозначим число ветвей схем буквой b и число узлов у. Для того чтобы получить линейно-независимые уравнения, по первому закону Кирхгофа составляется число уравнений, равное числу узлов минус единица, т.е. у- 1. По второму закону Кирхгофа составляется число уравнений, равное числу ветвей за вычетом числа уравнений, составленных по первому закону Кирхгофа, т.е.

b – (у – 1).

При составлении уравнений по второму закону Кирхгофа необходимо следить за тем, чтобы были охвачены все ветви схемы.

Рассмотрим применение законов Кирхгофа для схемы рис. 1.9. Произвольно выбираем положительные направления токов и обозначаем их на схеме. В схеме два узла, следовательно, по первому закону Кирхгофа достаточно составить только одно уравнение:

I ₁ + I ₂ = I ₃.

По второму закону Кирхгофа необходимо составить b – (у – 1) = 3 – (2 – 1) – 2 уравнения. Положительные направления обхода контуров выбираем по часовой стрелке.

Для контура R ₁ E ₁ R ₂ E ₂ : I ₁ R ₁ – I ₂ R ₂ = E ₁ + E ₂.

Знак «плюс» перед I ₁ R ₁ взят потому, что направление тока I ₁ совпадает с направлением обхода контура. Знак «минус» перед I ₂ R ₂ – потому, что направление I ₂ встречно обходу контура. Для контура Е ₂ R ₂ R ₃ R ₄:

I ₂ R ₂ + I ₃ (R ₃ + R ₄) = – E ₂ .

Поскольку положительные направления токов выбираются произвольно, то в результате расчета один или несколько токов могут оказаться отрицательными, т.е. в реальной схеме эти токи протекают в обратном направлении.

На основании закона сохранения энергии количество тепла, выделяющегося в единицу времени в резисторах схемы, должно равняться энергии, доставляемой за это же время источником питания:

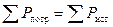
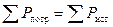или

или

Мощность потребителей вычисляется по следующим формулам:

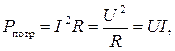
где: R – сопротивление потребителя;

I – ток, проходящий по потребителю;

U – напряжение на потребителе.

Например, для схемы рис. 1.10 уравнение баланса мощностей имеет вид:

I² (R ₁ + R ₂ + R ₃) = (E ₁+ E ₂) I.

Если схема питается не только от источников э.д.с, но и от источников тока, то при составлении энергетического баланса необходимо учитывать энергию, доставленную источниками тока.

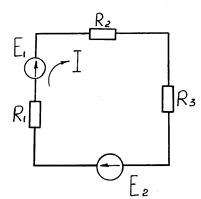
Рис.1.10. Цепь постоянного тока с двумя источниками питания

и тремя потребителями

Дата добавления: 2014-01-06