Комплексный метод расчета цепей переменного тока

Тригонометрическая форма расчета электрических цепей практически применима только для простейших цепей, не содержащих большого числа контуров и источников, поэтому широкое применение получил алгебраический метод, позволяющий рассчитывать цепи переменного тока аналогично цепям постоянного тока – комплексный метод (метод комплексных амплитуд, или символический метод).

Комплексное число, соответствующее точке, в которой лежит конец вектора (рис. 2.16), может быть записано в следующих формах: алгебраической 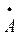= a ₁ + ja ₂; тригонометрической 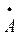= a (cos α + j sin α); показательной 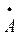= a·e^jα и полярной (угловой) 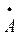= a · ∟α,

где: a ₁ = a ·cos α = Re[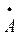] – действительная (вещественная) часть комплексного числа ;

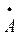a ₂ = a ·sin α = Im[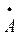] – мнимая часть комплексного числа;

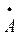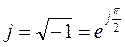– мнимая единица, или оператор поворота на угол

Рис. 2.16. Изображение вектора на комплексной плоскости

π/2 = 90° (умножение на j сводится к повороту вектора против часовой стрелки на угол π/2, а умножение на 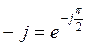к повороту вектора на прямой угол по часовой стрелке);

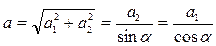– модуль комплексного числа (всегда положителен);

– угол или аргумент комплексного числа.

Показательная форма записи комплексного числа получается из формулы Эйлера:

cos α ± j ·sin α = e^±jα

Комплексное число 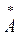= a ₁ – ja ₂ = ae^-jα называется комплексно-сопряженным числу 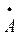= a ₁ + ja ₂ = ae^jα. Произведение компексно-сопряженных чисел – число действительное, равное квадрату их модуля:

.

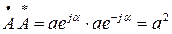Умножение комплексного числа ae^jα на число е^jφ сводится к повороту вектора а в комплексной плоскости на угол α + φ:

ae^jα · e^jφ = ae^j(α+φ).

Сложение и вычитание комплексных чисел производится в алгебраической форме:

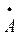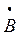+ = (a₁ + ja₂) ± (b₁+ jb₂) = (a₁±b₁) + j(a₂±b₂).

Умножение и деление комплексных чисел может производиться в алгебраической и показательной формах:

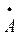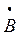· = (a₁ + ja₂)· (b₁+ jb₂) = (a₁b₁ – a₂b₂) + j (a₂b₁ + a₁b₂) = ae^jα · be^jβ = abe^{j(α+β )} .

.

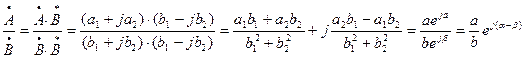Возведение в степень производится следующим образом:

(ae^jα)ⁿ = aⁿe^jαn = aⁿ (cosαn + jsinαn).

Рассмотрим проекции вращающегося против часовой стрелки с постоянной угловой скоростью ω вектора 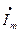(рис. 2.17). Проекция на действительную ось – I_m cos α. Проекция на мнимую ось – jI_m sin α.

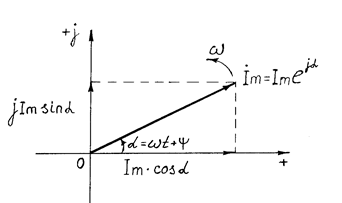
Рис. 2.17. Проекции вращающегося вектора 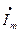на комплексную плоскость

Тогда согласно формуле Эйлера

I_m e^jα = I_m cosα + jI_m sinα.

Угол α может быть любым. Если α = ωt + ψ, где ψ – начальная фаза, то

I_m e^j(ωt+ψ) = I_m cos (ωt + ψ) + jI_m sin (ωt + ψ),

где: I_m cos (ωt + ψ) – действительная часть комплексного числа;

jI_m sin (ωt + ψ) – мнимая часть комплексного числа.

Для единообразия принято на комплексной плоскости изображать векторы синусоидально изменяющихся во времени величин для момента времени ωt = 0. Для этого момента времени вектор I_m e^j(ωt+ψ) будет равен I_m e^jψ = 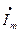, где 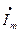– комплексная амплитуда тока, модуль ее равен 1_т, а угол α на комплексной плоскости равен начальной фазе ψ. Аналогично можно записать для э.д.с. и напряжения:

Например, если ток, протекающий по цепи, равен i = 12sin (ωt + 30°)А, то в данном случае I_m = 12 А, ψ = 30º, следовательно, комплексная амплитуда тока 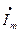= 12 e^j30º, а комплекс тока (комплексный ток)

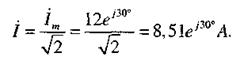
Дата добавления: 2014-01-06