Синтаксическая мера информации

Количественные характеристики информации

Лекция 3. Количество и качество информации

Виды информации

Можно выделить следующие виды информации

По восприятию органами чувств:

· звуковая (аудиальная)

· визуальная (символы, рисунки, жесты, зрительные образы)

· органолептическая

· вкусовая

· обонятельная (запахи)

· тактильная (ощущения)

По общественному назначению:

· массовая;

· личная (хранится в памяти каждого человека);

· общественно – политическая;

· обыденная;

· эстетическая.

Специальная:

· научная;

· техническая;

· отраслевая;

· производственная;

По области возникновения:

· элементарная (процессы явлений неодушевленной природы);

· биологическая (процессы животного и растительного мира);

· социальная (человеческое общество).

Эта мера количества информации оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту. На синтаксическом уровне учитываются тип носителя и способ представления информации, скорость передачи и обработки, размеры кодов представления информации.

Объём данных (V_Д) понимается в техническом смысле этого слова как информационный объём сообщения или как объём памяти, необходимый для хранения сообщения без каких-либо изменений.

Информационный объём сообщения измеряется в битах и равен количеству двоичных цифр (“0” и “1”), которыми закодировано сообщение.

В компьютерной практике слово “бит” используется также как единица измерения объёма памяти. Ячейка памяти размером в 1 бит может находиться в двух состояниях (“включено” и “выключено”) и в неё может быть записана одна двоичная цифра (0 или 1). Понятно, что бит — слишком маленькая единица измерения информации, поэтому пользуются кратными ей величинами. Основной единицей измерения информации является байт. 1 байт равен 8 битам. В ячейку размером в 1 байт можно поместить 8 двоичных цифр, то есть в одном байте можно хранить 256 = 2⁸ различных чисел. Для измерения ещё бóльших объёмов информации используются такие величины:

1 Килобайт =	2^10байт =	1024 байт
1 Мегабайт =	2^10 Килобайт =	1024 Килобайт
1 Гигабайт =	2^10 Мегабайт =	1024 Мегабайт
1 Терабайт =	2^10Гигабайт =	1024 Гигабайт

Пример 1. Важно иметь представление, сколько информации может вместить килобайт, мегабайт или гигабайт

· При двоичном кодировании текста каждая буква, знак препинания, пробел занимают 1 байт.

· На странице книги среднего формата примерно 50 строк, в каждой строке около 60 символов, таким образом, полностью заполненная страница имеет объём 50 x 60 = 3000 байт ≈3 Килобайта.

· Вся книга среднего формата занимает ≈ 0,5 Мегабайт. Один номер четырёхстраничной газеты — 150 Килобайт. Если человек говорит по 8 часов в день без перерыва, то за 70 лет он наговорит около 10 Гигабайт информации.

· Один чёрно-белый кадр (при 32 градациях яркости каждой точки) содержит примерно 300 Кб информации, цветной кадр содержит уже около 1 Мб информации.

· Телевизионный фильм продолжительностью 1,5 часа с частотой 25 кадров в секунду — 135 Гб.

Количество информацииI на синтаксическом уровне определяется через понятие энтропии системы.

Пусть до получения информации потребитель имеет некоторые предварительные (априорные) сведения о системе α. Мерой его неосведомленности о системе является функция H(α), называемая энтропией системы, которая в то же время служит и мерой неопределенности состояния системы.

После получения некоторого сообщения β получатель приобрел некоторую дополнительную информацию I_β(α), уменьшившую его априорную неосведомленность так, что неопределенность состояния системы после получения сообщения β стала H_β(α).

Тогда количество информации I_β(α) ξ системе, полученной в сообщении β, определится как

I_β(α)=H(α)-H_β(α).

т.е. количество информации измеряется изменением (уменьшением) неопределенности состояния системы. Если конечная неопределенность H_β(α) обратится в нуль, то первоначальное неполное знание заменится полным знанием и количество информации I_β(α)=H(α). Иными словами, энтропия системы Н(а) может рассматриваться как мера недостающей информации.

Энтропия H(α) системы α, имеющей N возможных состояний, согласно формуле Шеннона, равна:

,

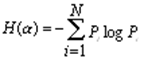где P_i — вероятность того, что система находится в i-м состоянии. Для случая, когда все состояния системы равновероятны, т.е. их вероятности равны P_i =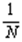, ее энтропия определяется соотношением

.

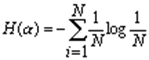Пример 2. Часто информация кодируется числовыми кодами в той или иной системе счисления, особенно это актуально при представлении информации в компьютере. Естественно, что одно и то же количество разрядов в разных системах счисления может передать разное число состояний отображаемого объекта, что можно представить в виде соотношения

N=mⁿ,

где N — число всевозможных отображаемых состояний;
m — основание системы счисления (разнообразие символов, применяемых в алфавите);
n —число разрядов (символов) в сообщении.

Допустим, что по каналу связи передается n-разрядное сообщение, использующее m различных символов. Так как количество всевозможных кодовых комбинаций будет N=m", то при равной вероятности появления любой из них количество информации, приобретенной абонентом в результате получения сообщения, будет

I = log N = n log m — формула Хартли.

Если в качестве основания логарифма принять m, то I = n. В данном случае количество информации (при условии полного априорного незнания абонентом содержания сообщения) будет равно объему данных I=V_Д, полученных по каналу связи.

Наиболее часто используются двоичные и десятичные логарифмы. Единицами измерения в этих случаях будут соответственно бит и дит.

Коэффициент (степень) информативности (лаконичность) сообщения определяется отношением количества информации к объему данных, т.е.

.

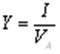С увеличением Y уменьшаются объемы работы по преобразованию информации (данных) в системе. Поэтому стремятся к повышению информативности, для чего разрабатываются специальные методы оптимального кодирования информации.

Дата добавления: 2014-01-06