Функции

Операторы

Операторы – это неотъемлемая часть математических выражений, вычисление которых является одной из основных задач MATLAB как системы, созданной для выполнения численных расчетов

Выражения используют обычные арифметические операции и правила стар­шинства.

+	сложение
-	вычитание
*	умножение
/	деление
\	левое деление
^	степень
‘	комплексно сопряженное транспонирование
()	определение порядка вычисления

Приоритет в выполнении арифметических операций обычный: сначала — возведение в степень, затем — умножение и деление, и потом — сложение и вычитание. Операции одинакового приоритета выполняются в порядке слева направо, но круглые скобки могут изменить этот порядок.

Помимо арифметических операций используются ещё операции отношения и логические операции.

Операции отношения сравнивают между собой два операнда по величине. Эти операции записываются следующими знаками или комбинациями знаков:

<	меньше
<=	меньше или равно
>	больше
>=	больше или равно
==	равно
~=	не равно

Последней группой операций являются логические операции:

&	И
|	ИЛИ
~	НЕ

Логические операции трактуют свои операнды как "истинные" (не равные нулю) или "ложные" (равные нулю). Если оба операнда операции "И" истинны (не равны нулю), то результат этой операции равен 1 ("истина"); во всех остальных случаях операция "И" вырабатывает значение 0 (ложь). Операция "ИЛИ" вырабатывает 0 (ложь) только в случае, когда являются ложными (равными нулю) оба операнда. Наконец, операция "НЕ" инвертирует "ложь" на "истину" и наоборот. То есть, если её операндом является ненулевое число, то эта операция вырабатывает 0, а если операнд нулевой, то тогда результатом применения операции "НЕ" будет единица.

Логические операции имеют самый низший приоритет.

В одном и том же выражении можно использовать все перечисленные операции: арифметические, логические и операции сравнения. Последовательность выполнения операций определяется их расположением внутри выражения, их приоритетом и наличием круглых скобок.

MATLAB предоставляет большое количество элементарных математических функций, таких как abs, sqrt, exp, sin. Вычисление квадратного корня или лога­рифма отрицательного числа не является ошибкой: в этом случае результатом является соответствующее комплексное число. MATLAB также предоставляет и более сложные функции. Боль­шинство из этих функций имеют комплексные аргументы.

Некоторые функции, такие как sqrt и sin - встроенные. Они являются частью MATLAB, поэтому они очень эффективны, но их вычислительные детали труд­но доступны. В то время как другие функции реализо­ваны в М-файлах. Поэтому вы можете легко увидеть их код и, в случае необхо­димости, даже модифицировать его.

Несколько специальных функций предоставляют значения часто используемых констант, таких как

pi	3.14159265...
i	мнимая единица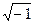
j	то же самое, что и i
eps	относительная точность числа с плавающей точкой, 2^-52
realmin	наименьшее число с плавающей точкой, 2^-1022
realmax	наибольшее число с плавающей точкой, 2^1023
Inf	бесконечность
NaN	не число

Бесконечность появляется при делении на нуль или при выполнении математи­ческого выражения, приводящего к переполнению, т.е. к превышению realmax. Не число (NaN) генерируется при вычислении выражений типа 0-0, которые не имеют определенного математического значения.

Имена функций не являются зарезервированными, поэтому возможно изменять их значения на новые, и далее использовать это значение в последующих вычислениях. Начальное значение может быть восстановлено следующим образом

Встроенные элементарные функции MATLAB включают тригонометрические, гиперболические, экспоненциальные и логарифмические функции, а также функции для работы с комплексными числами и для округления различными способами.

Ниже приведены основные стандартные функции вещественного аргумента.

Экспоненциальные функции
a^x	Степенная функция
x^a	Показательная функция
sqrt(x)	Квадратный корень
exp(x)	Экспонента
log(x)	Натуральный логарифм
log10(x)	Десятичный логарифм
abs(x)	Модуль
fix(x)	Отбрасывание дробной части числа
floor(x)	Округление до меньшего целого
round(x)	Обычное округление
ceil(x)	Округление до большего целого
rem(x,y)	Остаток от деления x на y без учёта знака
mod(x,y)	Остаток от деления x на y с учётом знака
sign(x)	Знак числа
factor(x)	Разложение числа x на простые множители

Тригонометрические функции
sin(x)	Синус
sinh(x)	Синус гиперболический
asin(x)	Арксинус
asinh(x)	Арксинус гиперболический
cos(x)	Косинус
cosh(x)	Косинус гиперболический
acos(x)	Арккосинус
acosh(x)	Арккосинус гиперболический
tan(x)	Тангенс
tanh(x)	Тангенс гиперболический
atan(x)	Арктангенс
atanh(x)	Арктангенс гиперболический
cot(x)	Котангенс
coth(x)	Котангенс гиперболический
acot(x)	Арккотангенс
acoth(x)	Арккотангенс гиперболический

Пример. Пусть требуется вычислить значение выражения

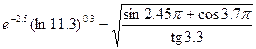
В соответствиями с правилами MATLAB это выражение будет записано следующим образом:

exp(-2.5)*log(11.3)^0.3-sqrt((sin(2.45*pi)+cos(3.78*pi))/tan(3.3));

Дата добавления: 2014-01-06