Обращение матрицы при помощи разбиения на блоки

Классический метод обращения матриц

Определение обратной матрицы классическим методом в практических ситуациях встречается редко. Тем не менее этот метод позволяет ясно представить общую взаимосвязь между элементами прямой и обратной матриц.

Общую технику определения А^-1 покажем на матрицах 3-го порядка.

Возьмем матрицу

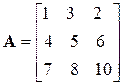
Для нахождения обратной к ней матрицы необходимо вначале определить

матрицу алгебраических дополнений .

Элементы этой матрицы вычисляются по формуле

,

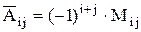где 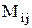- минор элемента .

Вычислим алгебраические дополнения для элементов первого столбца:

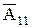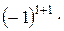= (5×10 - 8×6) = 2

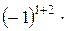= (4×10 - 7×6) = 2

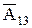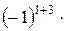= (4×8 - 7×5) = -3

Произведя аналогичные действия над элементами 2-й и 3-й строк, получаем матрицу алгебраических дополнений:

.

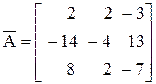Транспонируя матрицу , получаем присоединенную матрицу:

.

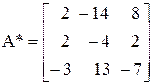Вычислим определить матрицы А:

.

Обратная матрица равна присоединенной матрице, умноженной на скаляр .

.

Наиболее просто вычисляется обратная матрица по отношению к диагональной матрице. Она также является диагональной, состоящей из обратных вели-

чин, расположенных на соответствующих местах главной диагонали:

.

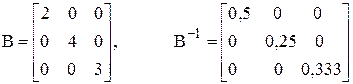Вычисление обратной матрицы часто может быть упрощено с помощью разделения ее на четыре подматрицы, причем верхняя левая и нижняя правая подматрицы должны быть квадратными.

Рассмотрим часто применяемый случай разделения матрицы, когда все четыре блока являются квадратными.

Пусть задана матрица четвертого порядка:

.

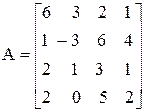Разделим матрицу A на блоки:

Произведем обращение подматрицы A₂₂:

= ×

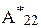
D = 3×2 - 5×1 = 1

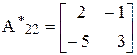
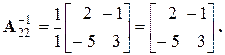
Определим блоки матрицы B, обратной матрице A:

.

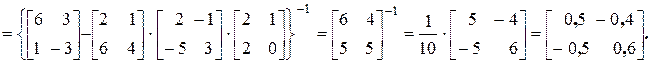
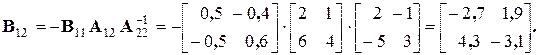
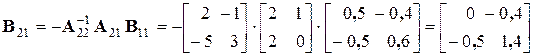Объединив полученные блоки, получаем обратную матрицу A^-1:

.

Дата добавления: 2014-01-06