Виды и способы организации выборки

Сущность и задачи выборочного метода

Статистическое исследование может осуществляться по данным несплошного наблюдения, основная цель которого состоит в получении характеристик изучаемой совокупности по обследованной ее части. Одним из наиболее распространенных в статистике методов, применяющих несплошное наблюдение, является выборочный метод.

Под выборочным понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой ее части на основе положений случайного отбора. При этом подлежащая изучению статистическая совокупность, из которой производится отбор части единиц, называется генеральной совокупностью (обозначается «N»). Отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью или просто выборкой ( обозначается «n»).

Значение выборочного метода состоит в том, что при минимальной численности обследуемых единиц проведение исследования осуществляется в более короткие сроки и с минимальными затратами труда и средств. Это повышает оперативность статистической информации, уменьшает ошибки регистрации.

По мере увеличения численности выборки показатели выборочной совокупности все более приближаются к показателям генеральной совокупности.

Задачи выборочного метода:

- получение наилучших оценок параметров генеральной совокупности;

- определение степени точности и надежности оценок, т.е. наличие возможности рассчитать ошибки выборки;

- снижение затрат труда и средств при выборочном обследовании.

Основными принципами выборочного метода являются:

1. Однородность, т. е. в выборочную совокупность должны попадать единицы, которые находятся в равных условиях и не сильно варьируют.

2. Принцип случайного отбора - обеспечения равной возможности единицам генеральной совокупности попасть в выборку (жеребьевка, тиражные машины, метод случайных чисел).

3. принцип типичной выборки – сознательный отбор, создающий уменьшенную копию, модель генеральной совокупности. Для этого предварительно проводится статистическая группировка единиц генеральной совокупности, затем пропорционально отбирается число единиц в выборочную совокупность.

4. Выборочная совокупность должна быть достаточно представительной, чтобы по ней судить о генеральной совокупности.

В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения.

Основным условием проведения выборочного обследования является предупреждение возникновения систематических ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности.

Существуют следующие виды формирования выборочной совокупности:

1) индивидуальный отбор — в выборку отбираются отдельные единицы;

2) групповой отбор — в выборку попадают качественно однородные группы или серии изучаемых единиц;

3) комбинированный отбор — это комбинация индивидуального и группового отбора.

Под способом отбора понимают порядок отбора единиц из генеральной совокупности. Различают два способа отбора: повторный и бесповторный. При повторном отборе каждая отобранная в случайном порядке единица после ее обследования возвращается в генеральную совокупность и при последующем отборе может снова попасть в выборку.

Способы отбора определяются правилами формирования выборочной совокупности.

Выборка может быть:

— собственно-случайная;

— механическая;

— типическая;

— серийная;

— комбинированная.

Собственно-случайная выборка состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки.

При этом 2 вида отбора:

- повторный

- бесповторный

Механическая выборка состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки.

Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке — каждая 20-я единица (1:0,05) и т.д.

Таким образом, в соответствии с принятой долей отбора, генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица.

Типическая выборка. При типической выборке генеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.

Серийная выборка. При серийной выборке генеральную совокупность делят на одинаковые по объему группы — серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию.

Комбинированный отбор – это сочетание различных способов отбора.

3.1 Статистическая оценка параметров выборочной совокупности

Пусть исследователь изучает количественный признак Х генеральной совокупности и имеет данные выборки, полученные в результате n независимых наблюдений: 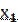, ,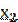…, 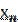. Положим, что выборка репрезентативная, т.е. достаточно хорошо воспроизводит генеральную совокупность. Рассматривая 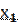, ,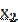…, 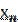как независимые случайные величины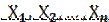, можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения признака Х – это значит, найти функцию от наблюдаемых случайных величин, которая и даёт приближённое значение оцениваемого параметра.

Оценкой 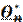параметра ϴ называется всякая функция результатов наблюдений над случайной величиной Х, с помощью которой судят о параметре ϴ:

Оценка 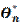называется несмещённой, если её математическое ожидание равно истинному значению параметра. В противном случае, она называется смещённой.

Часто полученная оценка бывает смещённой, но её можно поправить так, чтобы она стала несмещённой.

Генеральной средней 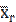называется среднее арифметическое значений признака генеральной совокупности, т.е.

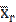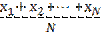=, если все значения 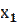, ,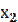…, 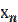признака генеральной совокупности объёма N различны и

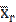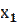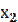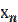=, если значения , ,…, признака имеют соответственно частоты 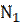, ,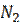…, , 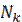причём 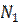++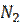…+ 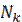= N.

Генеральную среднюю называют иначе математическим ожиданием признака Х.

Несмещённой оценкой математического ожидания случайной величины Х является выборочная средняя .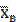

Выборочной средней называется среднее арифметическое значений признака выборочной совокупности, т.е.

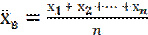, если все значения 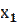, ,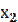…, 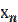признака выборки объёма n различны и

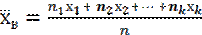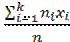=, если значения 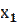, ,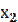…, 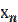признака имеют соответственно частоты 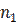, ,…, , 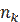причём 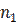++…+ 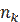= n.

Пример 1. Произведено шесть измерений (без систематических ошибок) некоторой случайной величины: a) 1, 3, 4, 5, 7, 8; b) 2, 3, 3, 3, 5, 8. Найти несмещённую оценку математического ожидания.

Решение.

a) Имеем выборку с различными вариантами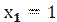, , , , 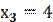,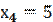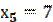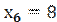. Тогда

= .

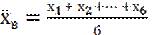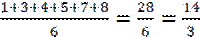b) Имеем выборку с вариантами 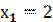, ,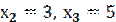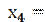8, которым соответствуют частоты 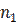===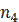1, 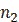=3. Тогда

.

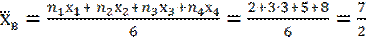Ответ: a) 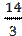, b) .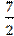

Пример 2. Имеется выборка генеральной совокупности объёма n=8:

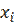
Несмещённая оценка математического ожидания равна 3,75. Найти недостающее значение варианты.

Решение.

Воспользуемся формулой 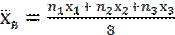, т.е. имеем 3,75=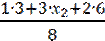, отсюда получаем 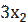=30-15, т.е. 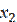=5.

Ответ: 5.

Генеральной дисперсией 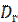называется среднее арифметическое квадратов отклонений значений признака генеральной совокупности от генеральной средней 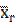, т.е. = .

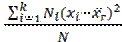Выборочной дисперсией 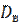называется среднее арифметическое квадратов отклонений значений признака выборочной совокупности от выборочной средней ,т.е. = .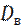

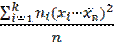Исправленной дисперсией 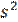называется произведение выборочной дисперсии на число 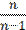, т.е. или =.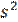

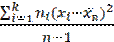Выборочная дисперсия является смещённой оценкой генеральной дисперсии, а исправленная – её несмещённой оценкой.

Пример. Имеетсявыборка генеральной совокупности объёма n=4:

Найти смещённую и несмещённую оценки дисперсии генеральной совокупности.

Решение.

Смещённой оценкой генеральной дисперсии служит выборочная дисперсия.

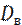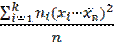= , где = .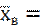

= .

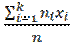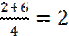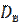Несмещённой оценкой генеральной дисперсии служит исправленная дисперсия .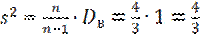

Ответ: , .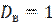

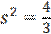Точечной оценкой параметра распределения называется оценка, определяемая одним числом.

Например, 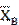- точечная оценка математического ожидания нормально распределённой случайной величины Х.

Интервальной оценкой называется оценка, определяемая интервалом, который с некоторой, как правило, большой вероятностью, задаваемой исследователем, накрывает неизвестное числовое значение параметра.

Если на основе выборки вычислена точечная оценка 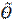параметра ϴ и число δ – ошибка оценки с заданной надёжностью γ=1-α (т.е. 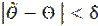), то интервал (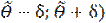является интервальной оценкой (доверительным интервалом) параметра ϴ. Доверительный интервал случаен, т.к. зависит от γ и от выборки. Не всегда удаётся получить доверительный интервал с границами, симметричными относительно оценки .

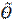Пример. Точечная оценка параметра a равномерного распределения равна 2,24. Тогда интервальной оценкой этого параметра может служить, например, интервал (2;5), и не может – интервал (2, 24; 5) или интервал (3; 5).

Интервальные оценки параметров нормального распределения

1. Доверительный интервал для оценки математического ожидания при известной дисперсии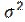имеет вид

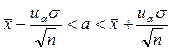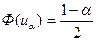где и 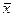- выборочная средняя, n – объём выборки, α=1-γ (γ – надёжность доверительного интервала).

2. Доверительный интервал для оценки математического ожидания при неизвестной дисперсии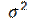имеет вид

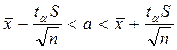, где 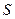- «исправленное» выборочное среднее

квадратическое отклонение, n< 30, находят по таблице Стьюдента с

надёжностью γ=1-α и числом степеней свободы k= n -1.

3. Доверительный интервал для оценки дисперсии при известном математическом ожидании имеет вид

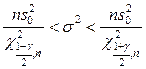, =- выборочная дисперсия повторной выборки, и - числа, находящиеся по таблице распределения хи-квадрат (n отвечает за количество степеней свободы, а и 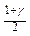- уровни значимости).

4. Доверительный интервал для оценки дисперсии при неизвестном математическом ожидании имеет вид

, - «исправленная» выборочная дисперсия.

Дата добавления: 2014-01-06