Основные определения

Граф определяется как множество двоек :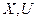
,

где:– конечное счётное множество всех вершин,

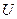– конечное счётное множество всех дуг графа.

Ориентированный граф (орграф) – граф, у которого рёбра ориентированы (со стрелками). Направленные рёбра называют дугами. Иначе граф неориентированный..

Граф, у которого вершины пронумерованы, называется помеченнымграфом.

Определение графа в терминах отображений:

Граф – это упорядоченная пара G = (X, Г),

где: Г: Х ® Х – отображение множества Х самого в себя.

Используя отображение, можно определить образы и прообразы:

Г (f) = { Æ } – вершина, несвязанная с другими вершинами;

Г (а) = {a} - множество всех вершин, смежных с а;

Г (с) = {в,d,e} - множество вершин, в которые идут дуги из с.

1 c

2 · 5

a · · 3 4 ·

b e

d· 6

7 · h

f ·

g ·

Рисунок 4.3 – Ориентированный граф

Вершины, связанные между собой в графе дугами, называются связанными вершинами.

Дуги, входящие в вершину и выходящие из вершины, называются инцидентными данной вершине.

Дуга, которая выходит из вершины и возвращается в неё, называется петлёй.

Граф, содержащий только часть дуг исходного графа, называется частичным графом.

Граф, содержащий лишь часть вершин исходного графа с относящемися к нему дугами, называется подграфом.

Взвешенный граф – граф, у которого каждой дуге поставлено в соответствие конкретное число - вес дуги 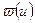, в частном случае это длина дуги .

Путь в графе 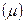– такая последовательность дуг, в которой конец предыдущей дуги совпадает с началом последующей: .

Петля – путь, состоящий из одной дуги.

Простой путь – путь, в котором каждая дуга встречается не более одного раза.

Цикл (контур) – путь, в котором начальная вершина совпадает с конечной: .

Длина пути – сумма длин дуг, составляющих данный путь:

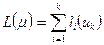
Полный граф – граф, в котором все вершины связаны друг с другом.

Связный граф – граф, в котором есть путь из любой вершины в любую.

Мультиграф – граф, у которого две вершины связаны более чем одной дугой.

Псевдограф – граф, который содержит петлю.

Изолированная вершина – вершина, которая не связана со всеми другими вершинами в графе.

· ·

· ·

Рисунок 4.4 – Полный граф

Двудольный граф – граф, у которого множество вершин является объединением двух непересекающихся множеств вершин 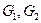, . Дуги могут объединять вершины различных множеств.

Ациклический граф – граф, не содержащий петель.

Каждому неориентированному графу можно поставить в соответствие ориентированный граф с тем же множест­вом вершин, в котором каждое ребро заменено двумя ориен­тированными дугами, инцидентными тем же вершинам и имеющими противоположные направления. Такое соот­ветствие называют каноническим.

Граф называется связным, если любые две его вершины соединены дугой.

Степенью (валентностью) вершины графа называется число инцидентных ей рёбер. Степень вершины 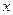обозначается: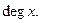

Список степеней вершин графа называется его степенной последовательностью.

Вершина называется тупиковой, если её степень равна 1.

Вершина называется изолированной, если её степень равна 0.

Вершина графа, смежная с каждой другой вершиной, называется доминирующей.

Граф назыввается регулярным, если степени его вершин равны.

Теорема. В графе с вершинами и 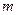дугами выполняется следующее соотношение:

,

где 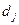– степень вершины.

Следствие 1. Число вершин в графе с нечётной степенью всегда чётно.

Следствие 2. Данная теорема характерна для графов без петель. Для графов с петлями необходимо считать, что петля добавляет 2 степени одной вершине.

Дата добавления: 2014-01-06