Эйлеровы графы

ОБХОДЫ В ГРАФАХ

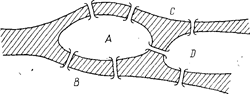
Начало теории графов как раздела математики связы­вают с так называемой задачей о кёнигсбергских мостах. Эта задача состоит в следующем. Семь мостов города Кёнигсберга были расположены на реке Прегель так, как изображено на рисунке.

Рисунок 4.20 – Кёнигсбергские мосты

Спрашивается, можно ли, выйдя из дома, вернуться обратно, пройдя в точности один раз по каж­дому мосту?

Сопоставим плану города граф , вершины которого соответствуют четырем разделяемым рекой участкам су­ши , а ребра — мостам. Этот граф изображен на рисунке 10.1.2. Видно, что некоторые пары вершин соединены двумя дугами, например, вершины А и В. Такие графы называются мультиграфами.

C

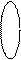A D

B

Рисунок 4.21 – Мультиграф

Задачу о кёнигсбергских мостах можно на языке теории графов сформулировать так:

есть ли в мультиграфе цикл, содержащий все ребра этого мультиграфа?

Эйлер доказал неразрешимость задачи о кёнигсберг­ских мостах. Он сформулировал и решил следующую общую проблему теории графов: при каких условиях связный граф содер­жит цикл, проходящий через каждое его ребро?

Цикл в графе называется эйлеровым, если он содер­жит все ребра графа по одному разу.

Связный граф, в котором есть эйле­ров цикл, называется эйлеровым графом. Такой граф мож­но нарисовать, не отрывая карандаша от бумаги и не повторяя линий.

Теорема Л. Эйлера (1736 г.):

Дата добавления: 2014-01-06