Алгоритм Краскала

Задача об остове минимального веса (о кратчайшем остове):

в связном взвешенном графе 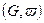порядка найти остов минимального веса.

Алгоритм Краскала, решающий эту задачу, заключа­ется в следующем.

1. Выбираем самое короткое ребро графа U1, затем ребро U2, затем самое короткое из оставшихся;

2. Из оставшихся ребер выбираем самое короткое ребро U3 так, чтобы оно не образовывало цикла с выбранными ребрами;

3. Продолжаем эту процедуру. На k-м к выбранным ребрам U1,…,Uк-1 добавляем самое короткое ребро из оставшихся ¦U¦-(к-1) ребер так, чтобы оно не образовывало цикла с выбранными ребрами;

4. При k=n-1 процесс заканчивается. Получим граф без циклов с (n-1)-м ребром. Построенный граф есть дерево, обозначим его T(n-1).

В графе, где некоторые ребра имеют одинаковую длину, кратчайшее частичное дерево может не быть однозначно определенным.

Следующая теорема утверждает, что алгоритм Краска­ла всегда приводит к остову минимального веса:

при i < n – 1 граф T_{i+ 1} всегда можно построить. Граф T_{n- 1} будет являться остовом минимального веса в графе (G,w).

Доказательство:

Граф T_i имеет ровно i ребер и потому при i < n – 1 является несвязным. А, так как, граф G связен, то в нем есть по меньшей мере одно ребро, не составляющее циклов с ребрами графа T_i. Итак, нужное ребро U_{i+ 1} существует и граф T_{i+ 1} можно построить.

Дата добавления: 2014-01-06