Оптимальное кодирование

Кодирование

Оптимальным кодированием называется процедура преобразования символов первичного алфавита m₁ в кодовые слова во вторичном алфавите m₂, при котором средняя длина сообщений во вторичном алфавите имеет минимально возможную длину.

Коды, представляющие первичные алфавиты с неравномерным распределением символов, имеющие среднюю минимальную длину кодового слова во вторичном алфавите, называются оптимальными неравномерными кодами (ОНК).

Эффективность ОНК оценивают при помощи двух коэффициентов:

1. коэффициента статического сжатия

,

который характеризует уменьшение количества двоичных знаков на символ сообщения при применении ОНК по сравнению с применением методов нестатистического кодирования.

2. коэффициента относительной эффективности

,

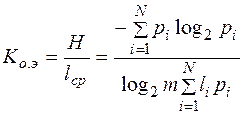который показывает, насколько используется статическая избыточность передаваемого сообщения.

Из свойств оптимальных кодов вытекают принципы их построения:

- выбор каждого кодового слова необходимо производить так, чтобы содержащееся в нем количество информации было максимальным,

- буквам первичного алфавита, имеющим большую вероятность, присваиваются более короткие кодовые слова во вторичном алфавите.

Принципы оптимального кодирования определяют методики построения оптимальных кодов.

I. Построение ОНК по методике Шеннона-Фано для ансамбля из M сообщений сводится к следующей процедуре:

1) множество из M сообщений располагают в порядке убывания вероятностей;

2) первоначальный ансамбль кодируемых сигналов разбивают на две группы таким образом, чтобы суммарные вероятности сообщений обеих групп были по возможности равны;

3) первой группе присваивают символ 0, второй группе символ 1;

4) каждую из подгрупп делят на две группы так, чтобы их суммарные вероятности были по возможности равны;

5) первым подгруппам каждой из групп вновь присваивают 0, а вторым - 1, в результате чего получают вторые цифры кода. Затем каждую из четырех подгрупп вновь делят на равные (с точки зрения суммарной вероятности) части и т. д. До тех пор, пока в каждой из подгрупп останется по одной букве.

Функция Med находит медиану указанной части массива Р [ b..e ], т.е. определяет такой индекс m (b ≤ m < e), что сумма элементов Р [ b..m ] наиболее близка к сумме элементов Р [ m + 1.. e ].

Примечание. При каждом удлинении кодов в одной части коды удлиняются нулями, а в другой части – единицами. Таким образом, коды одной части не могут быть префиксами другой. Удлинение кода заканчивается тогда и только тогда, когда длина части равна 1, то есть остается единственный код. Таким образом, схема построения префиксная, а потому разделимая, т.е. коды не требуют разделителя.

Пример: Построим оптимальный код сообщения, состоющего из восьми равновероятных букв.

Решение. Так вероятности данного ансамбля сообщений равны p₁ = = p₂ =...= p₈ = 2^-3 и порядок их расположения не играет роли, то расположим их так, как показано в таблице 2.1.1. Затем разбиваем данное множество на две равновероятные группы. Первой группе в качестве первого символа кодовых слов присваиваем 0, а второй - 1. Во второй колонке таблицы записываем четыре нуля и четыре единицы. После чего разбиваем каждую из групп еще на две равновероятные подгруппы. Затем каждой первой подгруппе присваиваем 0, а второй - 1 и записываем в третью колонку таблицы. Далее каждую из четырех подгрупп разбиваем на две равновероятные части и первой из них присваиваем 0, а второй - 1. Таким образом в четвертой колонке появится значение третьего символа кодовых слов.

Таблица 5.4 – Оптимальный код равновероятных букв

Буква	Кодовое слово полученное после разбиения
	первого	второго	третьего
А1 А2 А3 А4 А5 А6 А7 А8

Проверка оптимальности кода осуществляется путем сравнения энтропии кодируемого (первичного) алфавита со средней длиной кодового слова во вторичном алфавите.

Для рассматриваемого примера энтропия источника сообщений

H = log₂ N = log₂ 8 = 3 бит/символ

а среднее число двоичных знаков на букву кода

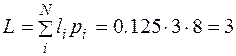бит

где l_i - длина i -ой кодовой комбинации; p_i - вероятность появления i -го символа комбинации длиной в l_i.

Таким образом, H = L, т. е. код является оптимальным для данного ансамбля сообщений.

Вывод: Для ансамблей равновероятных сообщений оптимальным является равномерный код. Если число исходных элементов ансамбля равно целой степени двух, то всегда H = L.

Пример. Первичный алфавит состоит из 8 символов со следующими вероятностями появления: a₁ = 0,5; a₂ = 0 ,25; a₃ = 0,098; a₄ = = 0,052; a₅ = 0,04; a₆ = 0,03; a₇ = 0,019; a₈ = 0,011. Построить ОНК по методу Шеннона - Фано и подсчитать коэффициенты.

Решение проиллюстрируем в таблице 5.5.

Таблица 5.5 – Оптимальный код неравновероятных букв

ai	pi	Кодовое слово после разбиения	Знаков	lipi
	0,5		-	-	-	-	-		0,5
	0,25			-	-	-	-		0,5
	0,098					-	-		0,392
	0,052					-	-		0,208
	0,04					-	-		0,16
	0,03						-		0,15
	0,019								0,114
	0,011								0,066

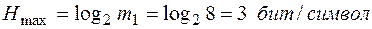
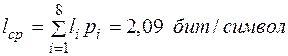
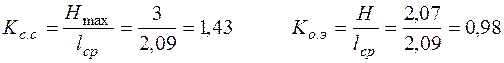
Недостатком методики Шеннона – Фано является неоднозначность построения ОНК. В методике Хаффмена этого недостатка нет.

ІІ. Хаффмен предложил следующий метод построения ОНК:

1) Символы первичного алфавита выписываются в порядке убывания вероятностей.

2) Последние n₀ символов, где 2 £ n₀ £ m и N - n₀ / m - 1 - целое число, объединяют в некоторый новый символ с вероятностью, равной сумме вероятностей объединяемых символов.

3) Последние символы с учетом образованного символа вновь объединяют и получают новый, вспомогательный, символ.

4) Опять выписывают символы в порядке убывания вероятноьстей с учетом вспомогательного символа и т. д. До тех пор, пока вероятности m оставшихся символов после N - n₀/m - 1-го выписывания не дадут в сумме 1.

На практике обычно не производят многократного выписывания вероятностей символов, а обходятся элементарными геометрическими построениями, суть которых для кодов с числом качественных признаков m = 2 сводится к тому, что символы кодируемого алфавита попарно объединяются в новые символы, начиная с символов, имеющих наименьшую вероятность, а затем, с учетом вероятностей вновь образованных символов, опять производят попарное объединение символов с наименьшими вероятностями и таким образом строят двоичное кодовое дерево, в вершине которого стоит символ с вероятностью 1.

Пример.

Построить методом Хаффмена оптимальный код для алфавита со следующим распределением вероятностей появления букв в тексте: A = 0,5; B = 0,15; C = 0,12; D = 0,1;

E = 0,04; F = 0,04; G = 0,03;

H = 0,02.

Решение.

Сначала находят буквы с наименьшими вероятностями 0,02 (H) и 0,03 (G), затем проводят от них линию к точке, в которой вероятность появления буквы G равна 0,05. Затем берут две наименьшие вероятности 0,04 (F) и 0,04 (E) и получают новую точку с вероятностью 0,08.

Теперь наименьшими вероятностями обладают точки, соответствующие вспомогательным символам с вероятностями 0,05 и 0,08. Соединяем их линией с новой точкой, соответствующей вспомогательному символу с вероятностью 0,13.

Продолжаем алгоритм до тех пор, пока линия от основных и вспомогательных символов не сольются в точке, дающую суммарную вероятность, равную 1.

Обозначим каждую верхнюю линию (см. рисунок 2.1.1) цифрой 1, а нижнюю - цифрой 0. Получим ОНК, который для каждого слова представляет собой последовательность нулей и единиц, которые встречаются по пути к данному слову от конечной точки (1,00).

Полученные коды представлены в таблице 5.6.

Таблица 5.6 – Двоичный код Хаффмена для восьми сообщений

Буква	Вероятность	ОНК	Число знаков в кодовом слове	pili
A B C D E F G H	0,50 0,15 0,12 0,10 0,04 0,04 0,03 0,02	0 0 1 0 1 1 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0		0,50 0,45 0,36 0,30 0,20 0,20 0,15 0,10

Пример.

Построить код Хаффмена для передачи сообщений при помощи трех частот f₁, f₂, f₃, если символы первичного алфавита встречаются в сообщениях со следующими вероятностями: А = 0,24; Б = 0,18; В = 0,38;

Г = 0,1; Д = 0,06; Е = 0,02; Ж = 0,02.

Решение.

Таблица 5.7 – Троичный код Хаффмена для семи сообщений

Буква	Вероятность	Дерево	Код
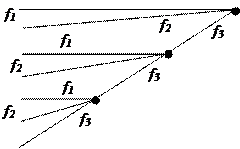В А Б Г Д Е Ж	0,38 0,24 0,18 0,1 0,06 0,02 0,02		f1 f2 f3f1 f3f2 f3f3f1 f3f3f2 f3f3f3

Полученный код легко декодируется, так как ни один код не начинается с f₁ и f₂, кроме одного одноразрядного кода.

К недостаткам алгоритма относятся:

1. Необходимость при кодировании двукратного прочтения файла первый раз для подсчета частоты вхождения символов,

второй – непостредственно для кодирования.

2. Необходимость хранения вместе с сжатым файлом декодирующего дерева для возможности восстановления файла.

Дата добавления: 2014-01-06