Рекурсивные функции

Первоначальной целью теории вычислимости (рекурсии) было придать строгость интуитивной идее вычислимой функции, т.е. функции, значения которой могут быть вычислены или автоматически или каким-либо другим эффективным способом

Рекурсивные функции уже в силу характера своего определения оказываются вычислимыми, т.к. каждая рекурсивная функция задается конечной системой равенств точно охарактеризованного типа в том смысле, что ее значения вычисляются с помощью этой системы равенств по точно формулируемым правилам, причем таким образом, что в итоге для вычисления значений заданной рекурсивной функции получается алгоритм определенного типа.

Очевидно, что к вычислимым функциям следует отнести все константы, т.е. все натуральные числа 0,1,2.... Нет необходимости включать в базис бесконечное множество констант. Достаточно 0 и функции следования f(x)= x+1, (x').

Кроме того в базис включается семейство функций тождества (или введения фиктивных переменных)

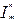(x1,...xn)=xm (m<=n)

Мощным средством получения новых функций из уже имеющихся является суперпозиция. Оператором суперпозиции называется подстановка

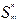(h,g1,...gm)=h(g1(x1,...xn)...gm(x1,...xn)).

Если заданы функции и операторы 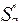, то можно считать заданными всевозможные операторы подстановки функций в функции, а также переименования, перестановки и отождествления переменных.

Оператором примитивной рекурсии 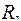называются подстановки, удовлетворяющие системе уравнений

f(x1,...,xn)= g(x1,...,xn)

f(x1,...,xn,y+1)= h(x1,...,xn,y,f(x1,...,xn,y)),

которая называется схемой примитивной рекурсии.

Функция называется примитивно-рекурсивной, если она может быть получена из константы 0, функции следования и функций 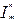с помощью конечного числа применений операторов суперпозиции 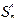и примитивной рекурсии .

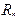В формально-индуктивном виде это определение выглядит следующим образом:

1. Функции 0, Х',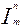для всех натуральных m и n являются примитивно-рекурсивными.

2. Если h,g1,...gm – примитивно-рекурсивные функции, то 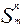– примитивно-рекурсивная функция.

3. Если g(x1,...xn),h(x1,...xm,y,z) – примитивно-рекурсивные функции, то 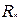– примитивно-рекурсивная функция.

4. Других примитивно-рекурсивных функций нет.

Примерами примитивно-рекурсивных функций являются

1. .

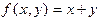2. .

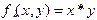3. .

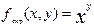Отношение R(x1,...xn) называется примитивно-рекурсивным, если примитивно-рекурсивна его характеристическая функция

.

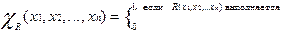Дата добавления: 2014-01-06