Статистическое определение вероятности события. Случаи неравновероятных исходов

.

Теорема. Вероятность события, противоположного событию равна

Доказательство. Пусть полная система равновозможных элементарных исходов содержит 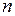событий, из которых 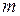(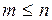), благоприятны событию 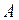. Тогда 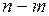исходов неблагоприятны событию 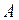, т.е. благоприятствуют событию . Таким образом,

.

Классическое определение вероятности предполагает, что

Ø число элементарных исходов конечно;

Ø эти исходы равновозможны.

Однако на практике встречаются испытания с бесконечным числом возможных исходов. Кроме того, нет общих методов, позволяющих результат испытания, даже с конечным числом исходов, представить в виде суммы равновозможных элементарных исходов. Поэтому применение классического определения вероятности весьма ограничено. Пример: кубик со смещенным центром тяжести.

Классическое определение вероятности имеет ограниченную применимость. Так, оно неприемлемо, если результаты испытания не равновозможны.

Во многих случаях более удобным оказывается статистическое определение вероятности, которое связано с понятием относительнойчастоты появления события 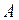в опытах. Относительная частота появления события 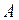– это отношение числа 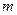появлений события 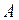в серии из 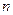опытов к числу испытаний:

.

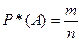Опыт показывает, что при проведении сравнительно малого числа испытаний относительная частота принимает значения, которые могут сильно отличаться друг от друга. При однотипных массовых испытаниях во многих случаях наблюдается устойчивость относительной частоты события, т.е. с увеличением числа испытаний относительная частота колеблется около некоторого постоянного числа , причем эти отклонения тем меньше, чем больше произведено испытаний.

Дата добавления: 2014-01-06