Понятие потока событий

Где.

Теорема Пуассона.

Теорема: Если вероятность 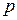наступления события 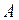в каждом испытании постоянна и мала, а число независимых испытаний 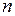достаточно велико, то вероятность того, что событие 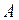наступит 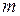раз, приближенно равна

,

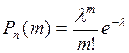Доказательство:

Введем обозначение 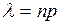, выразим отсюда 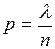и подставим это выражение в формулу Бернулли:

.

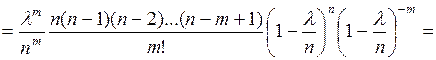
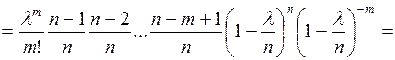
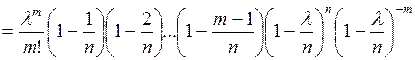При 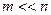все выражения в скобках, за исключением предпоследнего, можно принять равными единице, т.е.

.

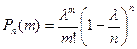При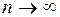

,

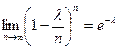поэтому

,

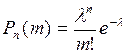что и требовалось доказать.

Формула Пуассона находит применение в теории массового обслуживания. Она может рассматриваться как математическая модель простейшего потока событий с интенсивностью 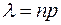. Параметр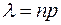представляет при этом среднее число успехов.

Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Интенсивностью потока 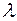называют среднее число событий в единицу времени. Простейшим (пуассоновским) называют поток событий, который обладает свойствами стационарности, отсутствия последействий и ординарности.

Свойство стационарности характеризуется тем, что вероятность 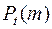появления 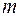событий на любом промежутке времени зависит только от числа 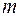и от длительности промежутка времени 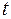и не зависит от начала его отсчёта.

Свойство отсутствия последействия характеризуется тем, что вероятность появления 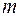событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка, т.е. предыстория потока не сказывается на вероятности появления событий.

Свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени маловероятно по сравнению с вероятностью появления только одного события.

Если интенсивность простейшего потока 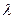известна, то вероятность появления 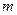событий за время 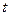определяется формулой

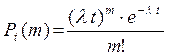
Пример простейшего потока событий. Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно трем. Найти вероятность того, что за 2 минуты поступит 4 вызова.

Подставляя в вышеприведенную формулу 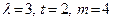, получим

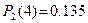
Дата добавления: 2014-01-06