Показательное распределение

Показательным (экспоненциальным) распределением непрерывной случайной величины 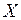называется распределение, имеющее плотность вероятности вида:

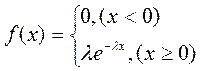
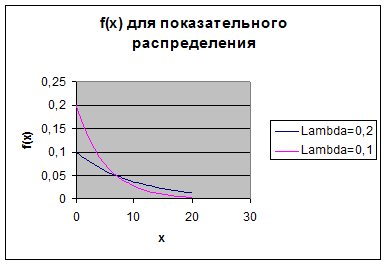
где 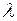– постоянная положительная величина. Плотность вероятностей для показательного распределения для 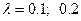приведена ниже

Функция распределения вероятности для показательного распределения имеет вид:

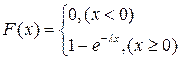
Функция распределения для 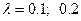приведена ниже

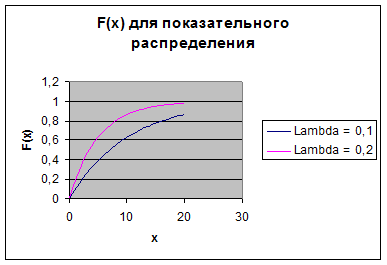
Можно показать, что математическое ожидание и дисперсия случайной величины, имеющей экспоненциальное распределение, равны:

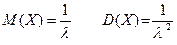
Пример. Установлено, что время горения электрической лампочки (Т) является случайной величиной, распределенной по показательному закону. Считая, что среднее значение этой величины равно 6 месяцам, найти вероятность того, что лампочка будет исправна более года.

Решение. Так как 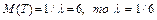и функция распределения случайной величины T имеет вид

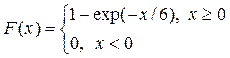
Поэтому

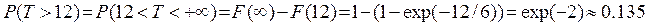
Лекция 9. Нормальное распределение. Вероятностный смысл входящих в него параметров. Функция Лапласа и ее свойства. Отклонение нормальной случайной величины от ее математического ожидания. Правило “трех сигм”

Непрерывная случайная величина 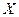имеет нормальный закон распределения с параметрам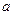и и 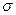, если ее плотность вероятности имеет вид функции Гаусса

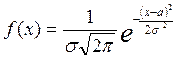
где 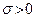. С помощью непосредственного вычисления математического ожидания и дисперсии нормального распределения легко выяснить вероятностный смысл его параметров: 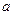– есть математическое ожидание, а 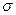- среднее квадратическое отклонение нормального распределения. При 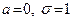распределение называется стандартным нормальным распределением.

Графики 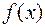для ряда конкретных значений математического ожидания и среднего квадратического отклонения приведены ниже.

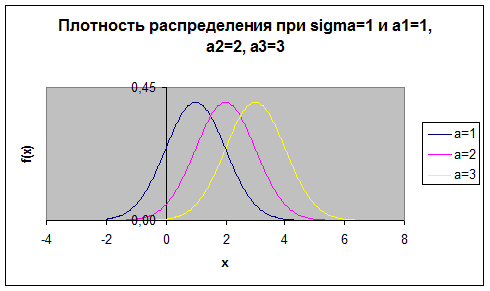
Рис. 1. Изменение вида функции 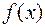при изменении математического ожидания

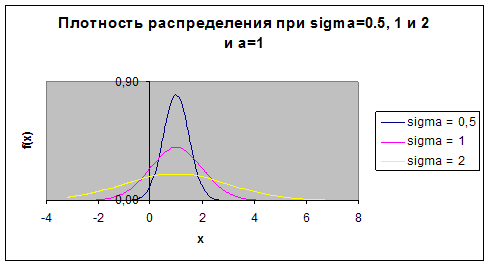
Рис. 2. Изменение 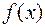при изменении среднего квадратического отклонения

Функция распределения в случае нормального распределения, очевидно, равна

.

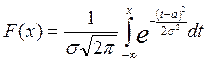Графики функции 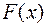для ряда значений математического ожидания и среднего квадратического отклонения изображены на приводимых ниже рисунках

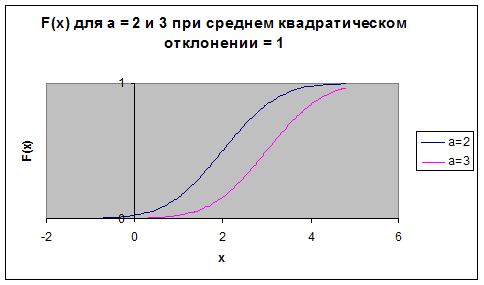
Рис. 3. Зависимость функции распределения от величины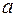

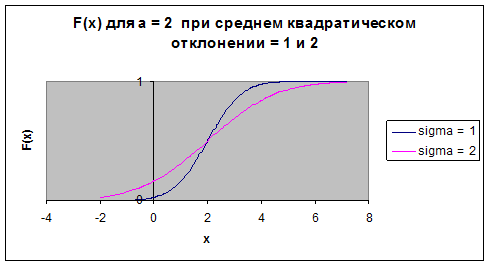
Рис. 4. Зависимость функции распределения от величины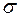

Нормальное распределение имеет исключительно важное значение для практических применений, так как многие непрерывные случайные величины описываются именно этим распределением. Оказывается, что суммирование большого числа случайных величин с различными законами распределения приводит к нормальному распределению результирующей суммы. Это свойство подтверждается центральной предельной теоремой (теорема Ляпунова). Смысл этой теоремы состоит в следующем. Если случайная величина 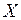представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то 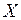имеет распределение, близкое к нормальному.

Следует иметь в виду, что при усилении влияния отдельных факторов могут появляться отклонения от нормального распределения результирующего параметра. Поэтому большое значение на практике уделяется экспериментальной проверке выдвинутых гипотез, в том числе и гипотезы о нормальном распределении.

Дата добавления: 2014-01-06