Решение. Магазин продает мужские костюмы

Пример 2.

Магазин продает мужские костюмы. По данным статистики известно, что распределение по размерам является нормальным с математическим ожиданием и средним квадратическим отклонением, равными 48 и 2 соответственно.

Определить процент спроса на 50-й размер, при условии разброса значений этой величины в интервале (49,51).

По условию, a=48, s = 2, a = 49, b =51. Используя формулу

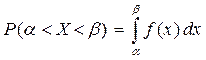
получаем, что вероятность спроса на 50-й размер в заданном интервале равна

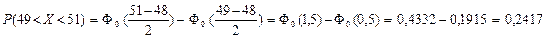
Вывод: спрос на 50-й размер составит примерно 24% и магазину нужно предусмотреть это в общем объеме закупки.

Лекция 10. Многомерные случайные величины. Совместная функция распределения двух случайных величин. Независимые случайные величины. Коррелированные случайные величины. Корреляционный момент и коэффициент корреляции.

До сих пор мы рассматривали случайные величины, возможные значения которых определялись одним числом (одномерные случайные величины). Например, число очков, которое может выпасть при бросании игральной кости (дискретная одномерная случайная величина) или расстояние от орудия до места падения снаряда (непрерывная одномерная случайная величина).

Часто приходится иметь дело с величинами, возможные значения которых определяются двумя или более числами. Такие величины называются n – мерными случайными величинами; n – мерную случайную величину можно рассматривать как систему n случайных величин. В данном контексте используется также термин многомерный случайный вектор 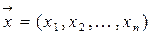, где каждая из величин 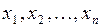называется составляющей (компонентой). Аналогично одномерным случайным величинам различают дискретные многомерные случайные величины (их составляющие дискретны) и непрерывные многомерные случайные величины, составляющие которых непрерывны.

Пример. Станок штампует стальные плитки. Если контролируемыми размерами являются длина X, ширина Y и высота Z плитки, то мы имеем трехмерную случайную величину (X,Y,Z).

Остановимся более подробно на двумерных случайных величинах.

Дата добавления: 2014-01-06