A. Понятие о корреляционном анализе

Лекция 16. Понятие о корреляционно-регрессионном анализе

Две или несколько случайных величин могут быть связаны либо функциональной, либо статистической (стохастической) зависимостью.

В экономике строгая функциональная зависимость реализуется редко, так как экономические показатели подвержены действию случайных, часто неконтролируемых факторов. Чаще имеет место так называемая статистическая зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, при изменении одной из величин может изменяться среднее значение другой.

Пример статистической зависимости: урожай зерна Y зависит от количества внесенных удобрений X. С одинаковых по площади участков при равных количествах внесенных удобрений снимают разные урожаи. Это связано с влиянием случайных факторов (осадки, температура воздуха и др.). Вместе с тем, средний урожай зависит от количества удобрений, т.е. Y связано с X статистической зависимостью.

При изучении статистических зависимостей различают корреляцию и регрессию. Основным методом исследования статистических зависимостей выступает корреляционно – регрессионный анализ.

Корреляционный анализ состоит в определении степени связи между случайными величинами.

Регрессионный анализ устанавливает формы зависимости между случайной величиной Y (зависимой переменной) и значениями одной или нескольких переменных величин X (независимыми переменными).

Одна из наиболее распространенных задач статистического исследования состоит в изучении связи между наблюдаемыми переменными. Знание взаимосвязей отдельных признаков дает возможность прогнозировать развитие ситуации при изменении конкретных характеристик объекта исследования. Основное содержание экономической политики, в конечном счете, может быть сведено к регулированию экономических переменных, осуществляемому на базе выявленной информации об их взаимовлиянии. Поэтому проблема изучения взаимосвязей показателей является одной из важнейших в статистическом анализе экономических систем.

Корреляция в широком смысле слова означает связь, соотношение между объективно существующими явлениями. Если случайные переменные причинно обусловлены, то имеется корреляция.

Корреляция может быть:

ü положительной или отрицательной;

ü в зависимости от числа переменных – простой или множественной;

ü в зависимости от формы связи – линейной или нелинейной.

Важнейшими задачами корреляционного анализа являются:

ü измерение силы связи двух или более факторов;

ü отбор факторов, оказывающих существенное влияние на результативный признак (зависимую переменную) на основании измерения тесноты связи между факторами.

В случае лишь одной независимой переменой X в качестве меры связи между ней и зависимой переменной Y служит коэффициент корреляции. Он оценивается по выборке объема n связанных пар наблюдений (x_i, y_i). В случае нескольких переменных необходимо последовательно вычислять коэффициенты корреляции по нескольким рядам числовых данных. Полученные коэффициенты сводят в таблицы, называемые корреляционными матрицами.

Корреляционная матрица представляет собой квадратную матрицу, на пересечении строки и столбца которой находится коэффициент корреляции между соответствующими переменными.

Если в результате 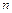испытаний система двух случайных величин 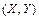приняла значения 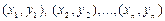, то коэффициент корреляции равен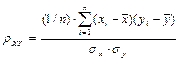

где 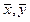- средние значения, а 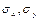- средние квадратические отклонения случайных величин 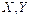соответственно.

Для многомерной выборки (т. е. в случае более двух факторов) необходимо рассчитать корреляционную матрицу 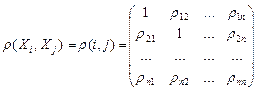,которая является симметричной относительно главной диагонали.

Дата добавления: 2014-01-06