Минимизация функций алгебры логики

Общая задача минимизации булевых функций может быть сформулирована таким образом: найти аналитическое выражение заданной булевой функции в форме, содержащей минимальное число букв. Эта задача достаточно хорошо исследована в классе дизъюнктивно – конъюнктивных форм.

Определение: Минимальной ДНФ булевой функции называется ДНФ, содержащая наименьшее число букв по отношению к другим ДНФ, представляющим заданную булеву функцию.

Определение: Булева функция q(x_1… x_n) называется импликантой булевой функции f(x_1… x_n) если для любого набора переменных, на котором, справедливо .

Определение: Импликанта 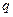булевой функции 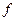, являющаяся элементарной конъюнкцией, называется простой, если никакая часть импликанты 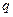не является импликантой функции .

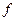1. Дизъюнкция любого числа импликант булевой функции 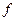так же является импликантой этой функции.

2. Любая булева функция 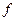эквивалентна дизъюнкции всех своих простых импликант. Такая форма называется сокращенной ДНФ.

Пример:

x1	x2	x3	f	q1	q2	q3	q4	q5	q6	q7

и простые импликанты.

Сокращенная ДНФ :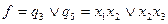

Импликанты и покрывают своими "1" все "1" функции .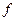

Получение сокращенной ДНФ является первым этапом отыскания минимальных форм булевых функций. Иногда из СкДНФ можно убрать одну или несколько простых импликант, не нарушая эквивалентности исходной функции. Такие простые импликанты называются лишними. Их исключение из СкДНФ – второй этап минимизации.

Определение: СкДНФ булевой функции называется тупиковой, если в ней отсутствуют лишние простые импликанты.

Тупиковые ДНФ булевых функций 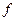, содержащие минимальное число букв, являются минимальными. МДНФ может быть несколько.

Дата добавления: 2014-01-06