Построение функциональной схемы автомата

На основании полученных выражений для булевых функций возбуждений элементов памяти автомата и булевых функций выходов автомата строятся КС функций возбуждения и КС формирования выходных сигналов. Элементы памяти подключаются к построенным КС. Функциональная схема автомата Мили при использовании Т-триггера представлена на рис. 1, D-триггера – на рис. 2, RS-триггера – на рис. 3, JK-триггера – на рис.4.

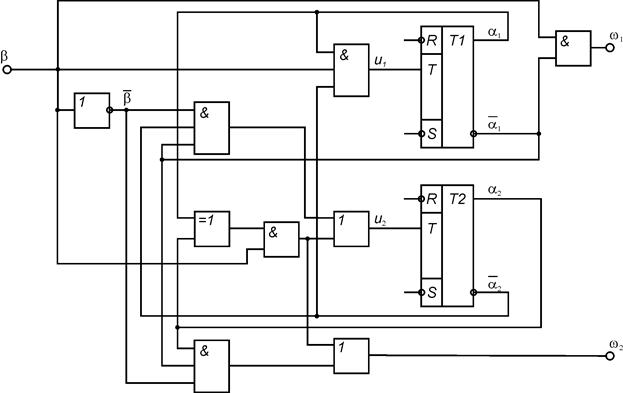
Рис. 12.5.

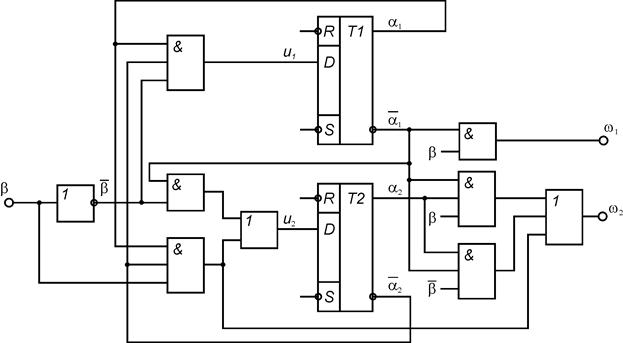
Рис. 12.6.

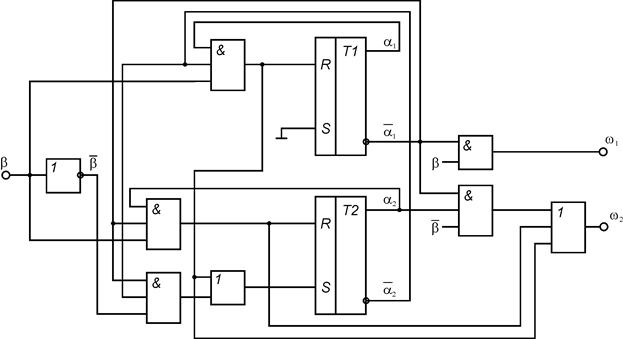
Рис. 12.7.

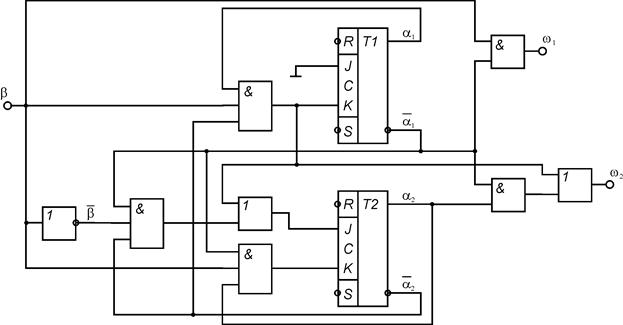
Рис. 12.8.

Глава 13

Обеспечение устойчивости функционирования ЦА

Обеспечение устойчивости функционирования ЦА с памятью – одна из главных задач этапа структурного синтеза. Под устойчивым функционированием ЦА понимают его функционирование в соответствии с таблицей переходов и выходов. Неустойчивая работа ЦА связана с особенностями физической реализации ЛЭ и элементов памяти его схемы, а так же различными величинами задержек распространения сигнала в элементах и КС.

По характеру физических сигналов, которые используются в ЦА может выделить три основных типа схем: потенциальные, импульсные и импульсно-потенциальные.

Потенциальные схемы может быть построены как на принципе естественного тактирование (асинхронные схемы), так и на принципе принудительного тактирование (синхронные схемы). При естественном тактировании выходы ЗЭ (элементов задержки) через схему обратной связи (составленную из ЛЭ) управляют своими собственными входами. Это создаёт возможность появления в схеме “гонок”. Суть гонок состоит в следующем: ЗЭ (элементы задержки) имеют различные, хотя и близкие времена срабатывания. Если по условиям срабатывания (таблице переходов) ЦА в какой-то момент времени должен изменить свое состояние сразу несколько ЗЭ, то между элементами начинаются гонки. Тот элемент, который выиграет эти гонки, то есть изменит свое состояние раньше, чем другие элементы, может через цепь обратной связи изменить сигналы на входах некоторых ЗЭ до того, как другие участвующие в гонке элементы изменят свое состояние. Это может вызвать переход автомата совсем не в то состояние, которое предусмотрено таблицей переходов автомата.

Проблему гонок может решить за счёт исключения необходимости одновремённого изменения состояний сразу у нескольких ЗЭ. С этой целью применяют противогоночное кодирование состояний ЦА, при котором (двоичные) коды любых двух соседних состояний (состояний переходящих одно в другое под воздействием какого-нибудь входного сигнала) отличаются друг от друга не более чем одним разрядом. Но противогоночное кодирование оказывается возможным далеко не во всех случаях.

Необходимость решения проблемы гонок и проблемы согласования переходов ЦА из одного состояния в другое с изменениями входных сигналов отпадает при введении принудительного тактирования автомата, то есть при превращение автомата в синхронный автомат. Для потенциальных схем принудительное тактирование осуществляется за счёт удвоения числа ЗЭ и введения тактового генератора.

Для асинхронных потенциальных схем, использующих ЗЭ с двумя выходами, существует опасность неправильного срабатывания, связанная с не одновременностью установления сигналов на прямом и на инверсном выходе после перехода ЗЭ из одного состояния в другое. В результате этого в какой-то момент времени может оказаться, что некоторая переменная х и её инверсия принимают одинаковые значения. Проблема устранения источников возникновения подобных ситуаций называется проблемой риска.

Риск неправильного срабатывания имеет место лишь для тех ЗЭ, которые должны сохранять свое состояние в течение рассматриваемого такта. Если это состояние – “1”, то говорят о риске в единице, если – “0”, то о риске в нуле.

Рассмотрим в качестве примера функцию 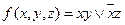. Для этого представления функции существует риск по переменной х. Функция f сохраняет значение “1” при изменении значения х, если y=1 и z=1, и сохраняет значение “0”, когда y=0, z=0. При одновременном обращении в “0” х и выбранное представление функции f дает нулевое значение при любых y и z, в том числе и при z=y=1. Таким образом имеется риск в единице по переменной х. При других представлениях функции f, например , риск по х и по всем другим переменным отсутствует.

Справедливы следующие утверждения.

1. при представлении булевой функции произвольной ДНФ отсутствует риск в “0”, а при представлении произвольной КНФ отсутствует риск в “1”.

Для существующих х произвольную ДНФ функции f может представить в виде: 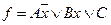, где А, В, С – булевые функции не зависящие от х. Если при каких-то фиксированных значениях всех переменных, отличных от х, функция f=0 как при x=0, так и при x=1, то это значит что A=В=С=0. Но тогда f=0 при 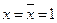так и при 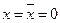. Таким образом риск в “0” по переменной х отсутствует. Однако остаётся возможность риска в “1”.

2. Представления булевой функции в виде СкДНФ и СкКНФ свободны от риска как в “0” так и в “1” по всем переменным. (Доказательство смотреть В.М.Глушков Синтез ЦА стр.356).

Таким образом при синтезе асинхронных потенциальных схем по соображениям надёжности иногда целесообразно отказаться от минимальных форм и пользоваться сокращенными.

Проблемы риска и гонок возникли лишь с появлением потенциальной элементной базы. Используемая ранее импульсно-потенциальная элементная база предусматривала применение статических триггеров со встроенной задержкой. При этом величина задержки была больше длительности импульсного сигнала поступающего на вход триггера. Таким образом переходные процессы формирования сигналов на выходах элементов памяти автомата начинались лишь после окончания входного импульсного сигнала и не оказывали воздействия на входы этих же элементов памяти по цепям обратной связи.

13.2 Проблема синтеза надёжных схем из ненадёжных элементов

Рассмотренные ранее методы синтеза схем ЦА исходят из задачи наиболее экономного расходования элементов, как ЗЭ так и ЛЭ. По самому определению наиболее экономной схемы она должна обладать тем свойством, что выход из строя любого её элемента вызывает выход из строя всей схемы в целом, потому что, если в схеме есть элементы, которые могут исключить, не нарушая работы схемы, то такая схема не будет минимальной по числу элементов, использованных при её построении.

Различают 2 вида неисправностей ЦА. Неисправность первого вида – отказ, состоит в том, что начиная с некоторого момента времени и во все последующие моменты времени элемент перестаёт функционировать или функционирует неверно. Второй вид неисправности – это мгновенная самоустраняющаяся неисправность, называемая сбоем. наступление сбоя означает, что элемент не сработал или неправильно сработал в течение одного такта работы автомата, но возникшая таким образом неисправность вовсе не должна сохраняться на протяжении последующих тактов.

Современные сложные электронные ЦА состоят из многих тысяч ЛЭ и ЗЭ, требования к надёжности их работы очень высоки (вероятность сбоя ЦА должно быть 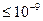), вероятность сбоя отдельных элементов 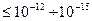. В ряде случаев требования к надежности элементов оказываются практически невыполнимыми, и тогда возникает проблема построения высоконадёжных схем из относительно ненадёжных элементов.

Методы на которых основано решение этой проблемы, сводятся к дублированию одних элементов другими, к многократному повторению, к автоматическому контролю и к исправлению работы отдельных участков схемы или всей схемы в целом.

Наиболее распространёнными является дублирование. Способ дублирования ЦА сводится к замене одного автомата двумя одинаковыми автоматами, выходы которых в процессе функционирования дублируемых автоматов постоянно сравниваются с помощью специальной схемы сравнения. Дублирование не учитывает внутреннюю структуру ЦА; с его помощью обнаруживаются ошибки любой кратности, возникающие на выходах одного из дублируемых устройств, а также ошибок, возникающие на выходах двух устройств одновременно, приводящие к появлению неодинаковых векторов выходов дублируемых устройств.

Недостатки дублирования:

- большая структурная избыточность требующая усвоения оборудования.

Пример: Продублировать ЦА А, имеющий три выходных канала .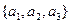

Состояние выходов продублированного устройства можно представить в виде матрицы G при контроле:

,линейный групповой код

а так называемая функция декодирования имеет вид:

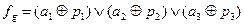
Дублирование можно осуществить не пространственным, а временным путём, то есть производить многократную прогонку входного слова через один и тот же ЦА и принимать в качестве верных лишь достаточно часто повторяющиеся результаты.

Другой распространённый метод – мажорирование. Мажорирование позволяет вырабатывать правильный выходной сигнал при наличии неисправностей в ЦА и определять место их появления с точностью до указания номеров неправильно работающих устройств. Мажорирование требует для своей организации использования нечётного числа устройств, работающих параллельно. Выработка правильного выходного сигнала устройства осуществляется мажоритарным ЛЭ. Для определения номеров неправильно работающих устройств необходимо дополнительно иметь специальный элемент анализа (ЭА).

Пример: Выполнить мажорирование для ЦА 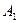с одним выходом .

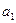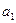
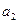
			f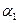

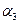
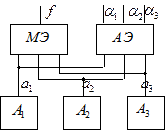
f – выход устройства, 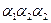- выходы элемента анализа.

для ЭА: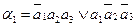

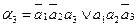
Недостаток метода – большая структурная избыточность.

С целью увеличения надёжности ЦА употребляются также специальные методы кодирования, позволяющие автоматически обнаруживать и даже исправлять ошибки, получающиеся в результате сбоев.

В большинстве современных ЦА информация делится на слова, имеющие определённую длину. Добавляя в коды этих слов новые разряды, и использовать их для хранения информации, позволяющей обнаруживать и исправлять ошибки в коде, возникающие в результате сбоев. Такие удлинённые коды являются избыточными, то есть они содержат большее число разрядов, чем необходимо для представления имеющейся информации.

Различают избыточные коды с обнаружением ошибок и избыточные коды с исправлением ошибок (самокорректирующиеся коды).

Простейший избыточный код – код с проверкой на чётность. Такой код получают путём добавления к слову одного контрольного разряда, в который записывают 0 или 1 с тем, чтобы число 1 в полученной кодовой комбинации было нечётным. Если, например, исходное слово А=10101100, то в коде с проверкой на чётность оно будет представлено как A`=101011001. Если А=10101101, то A`=101011010.

Таким образом любая ошибка нечётной кратности обнаруживается этим кодом.

К кодам с исправлением ошибок относятся коды Хэмминга, предназначенные для исправления одной ошибки или обнаружения двух и исправления одной ошибки. (см. К.Г.Самофалов ЭЦВМ стр.466).

Дата добавления: 2014-01-06