Граф-схемы алгоритмов

ГСА называется ориентированный граф, содержащий одну начальную вершину (Начало), одну конечную вершину (Конец) и произвольное конечное множество условных и операторных вершин. Любая вершина ГСА, кроме вершины «Начало» имеет по одному входу. Вершина «Начало» входов не имеет. Вершина «Начало» и любая операторная вершина имеют по одному выходу. Вершина «Конец» выходов не имеет. Любая условная вершина имеет два выхода, помеченных символами «Да» и «Нет», либо «1» и «0» соответственно.

ГСА должен удовлетворять следующим условиям:

1. Входы и выходы вершин соединяются друг с другом с помощью дуг, направленных от выхода к входу.

2. Каждый выход соединен только с одним входом.

3. Любой вход соединяется, по крайней мере, с одним выходом.

4. Любая вершина ГСА лежит хотя бы на одном пути от «Начало» в «Конец».

5. Один из выходов условной вершины может соединяться с ее входом, что недопустимо для операторной вершины.

6. Разрешается в различных условных вершинах записывать одинаковые логические условия.

7. В каждой операторной вершине записывается оператор, представляющий собой выходной сигнал или совокупность выходных сигналов УА. Разрешается в различных операторных вершинах записывать одинаковые операторы.

Будем называть микропрограммнымавтоматом конечный автомат Мили или Мура, построенный по граф-схеме алгоритма. При построении микропрограммного автомата считают, что его входной алфавит совпадает с множеством сигналов логических условий, выходной алфавит – с множеством сигналов выполнения отдельных микроопераций, а алфавит состояний и функций переходов задается графом автомата. Работа такого автомата тактируется генератором синхросигналов, причем период 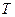следования этих сигналов 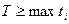, где 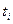- время, необходимое для выполнения i -й микрооперации.

Обычно при проектировании различных устройств предварительно составляется так называемая содержательная ГСА, в которой внутри условных и операторных вершин записаны логические условия и микрооперации в содержательных терминах.

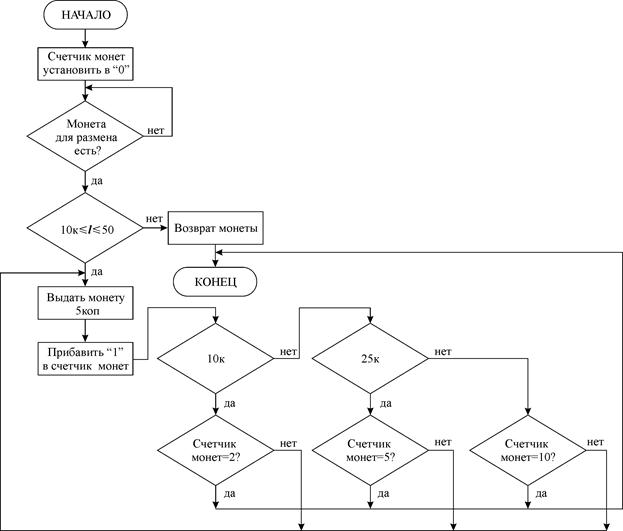
Пример. Построить содержательную ГСА УА по размену металлических денег. При этом будем считать, что можно разменивать монеты достоинством 10, 25, 50 коп. на соответствующее число 5 коп. монет. Будем полагать, что в качестве операционных автоматов используются:

блок анализа стоимости размениваемых монет;

блок выдачи монет;

блок анализа наличия монет;

счетчик монет.

Чтобы на основе содержательной ГСА получить необходимый набор состояний микропрограммного автомата прибегают к так называемой отметке ГСА.

Правила построения отмеченной ГСА различны для автоматов Мили и Мура.

Если необходимо построить микропрограммный автомат Мили, то содержательная ГСА УА размечается в соответствии такими правилами:

1) символом 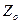отмечают вход первой вершины, следующей за вершиной «Начало». А также вход вершины «Конец»;

2) входы вершин (операторных или условных), следующих за операторными вершинами, отмечают символами ,…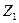

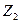3) входы двух различных вершин, за исключением вершины «Конец», отмечаются различными символами;

4) вход вершины может отмечаться только одним символом;

5) содержательные термины микроопераций и логических условий заменяются их условными обозначениями.

После разметки ГСА УА по размену денег примет вид:

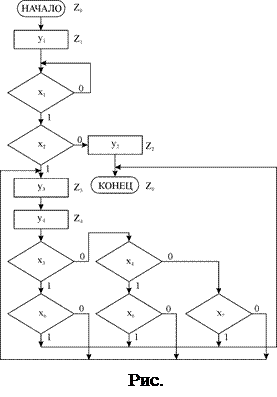
Если необходимо построить автомат Мура, то разметку делают т.о.:

1) символом 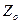отмечают вершины «Начало» и «Конец»;

2) различные операторные вершины отмечаются различными символами ,…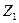

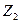3) все операторные вершины должны быть отмечены.

Вид отмеченной ГСА для УА по размену денег представлен на рис. 3.

После полученной отмеченной ГСА строится граф автомата Мили или Мура. Он имеет столько различных вершин, сколько различных букв 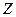с индексами имеется в отмеченной ГСА. Между двумя вершинами графа имеется дуга, если на отмеченной ГСА между этими вершинами есть путь. Над дугой ставится входной сигнал, равный конъюнкции логических условий (и синхросигнала) соответствующего пути. Если путей несколько, то входной сигнал представляет из себя дизъюнкцию конъюнкций. Если строится граф автомата Мура, то символы микроопераций (т.е. выходные сигналы управляющего автомата) записываются около соответствующих вершин. Если в отмеченной ГСА имеется безусловный переход между операторными вершинами, то на графе автомата ставится входной сигнал «1», показывающий, что данный переход происходит при поступлении очередного синхросигнала.

Граф автомата Мили приведен на рис. 4, граф автомата Мура на рис. 5. Дальнейший синтез производится с помощью метода структурного синтеза.

Для построения функциональной схемы автомата Мили составим таблицу переходов-выходов (табл. 1). Кодирование входных сигналов, состояний и выходных сигналов осуществим по таблицам 2, 3, 4 соответственно.

Каждому логическому условию ГСА можно поставить в соответствие физическую одноразрядную шину, считая, что логическое условие есть выходной сигнал определенного ОА. Так «1» на шине 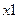будет означать, что монета поступила в блок анализа наличия монет, и он информирует об этом УА. Т.о. двоичный вектор будет представлять совокупный входной сигнал УА, а сигналы 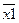, , , , 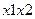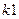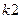могут быть получены с помощью специальной КС формирования входных сигналов.

Для выходных сигналов автомата 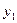, , 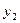, 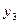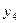чаще удобней использовать также отдельные физические шины. Такая организация выходных каналов автомата целесообразна, если операционные автоматы, которыми управляет синтезируемый автомат, физически разнесены. Кодирование выходных сигналов в соответствии с табл. 4 требует их дешифрации в блоке ОА.

Структурная таблица переходов-выходов УА представлена в табл. 5. В качестве элементов памяти выберем Т-триггеры. Таблица функций возбуждения синтезируемого автомата имеет вид табл. 6, а функции возбуждения 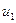и 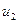представлены в ДНФ. Функции выходов могут быть получены по табл. 5 или табл. 7.

Микропрограмма, отражающая алгоритм функционирования автомата, может быть записана в ЗУ, чаще всего ПЗУ. При этом могут иметь место некоторые особенности при адресации и кодировании микрокоманд.

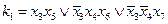
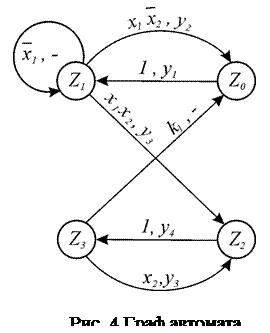
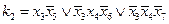
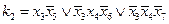
Таблица 1

Состояния автомата	Входные сигналы

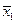
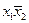
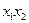
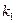
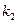
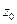
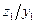
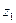
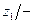
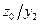
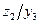
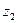
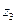
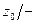
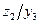
Таблица 2

Входные сигналы автомата	Код входных сигналов

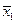
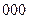
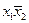
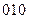
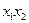
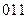
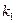
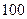
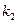
Таблица 3

Состояния автомата	Код состояний

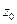
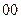
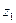
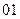
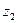
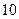
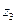
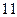
Таблица 4

Выходные сигналы автомата	Код выходных сигналов

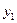
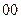
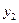
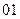
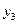
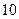
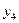
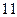
Таблица 5

Состояния автомата	Входные сигналы

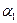
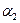
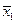
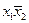
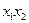
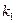
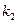
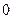
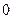
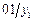
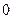
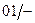
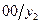
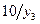
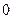
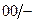
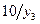
Таблица 6

Состояния автомата	Входные сигналы

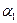
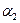
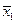
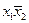
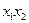
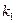
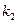
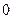
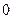
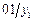
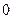
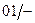
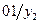
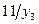
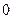
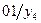
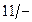
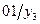
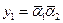
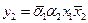
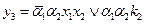
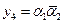
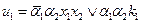
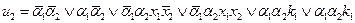для Т-триггера.

Таблица 7

Состояния автомата

Входные сигналы

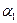
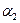
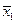
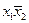
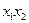
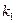
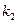
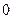
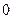
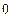
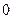
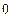
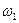
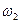
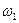
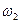
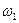
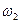
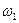
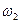
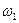
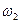
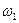
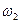
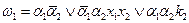
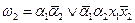
Порядок выполнения микрокоманд определяется логическими условиями, поступающими извне, в частности от ОА. Для того, чтобы реализовать процедуру выбора адреса следующей микрокоманды (в зависимости от значений переменных, отражающих условия) к ПЗУ добавляется схема выбора адреса, суть работы которой в следующем.

Логических условий может быть несколько и в двоичном коде команды обычно отмечаются «1» лишь те из них, которые подлежат анализу при переходе к следующей операции. Если передача управления не зависти от логических условий, переход является безусловным. Т.о. микрокоманда включает в себя информацию о выполняемых микрооперациях и анализируемых логических условий. Если в каждой микрокоманде указывается еще и адрес следующей микрокоманды, то такой способ адресации называется принудительным. Структура такой микрокоманды может быть представлена так:

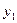
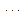
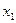
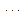
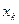
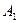
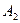
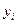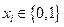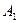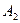, , ,двоичные адреса, разрядность которых определяется емкостью ПЗУ. После выполнения микрокоманды управление передается микрокоманде с адресом 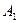или 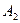в зависимости от значения анализируемой переменной .

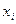Другая организация адресации предусматривает естественный способ смены адресов микрокоманд (с помощью счетчика), и лишь при выполнении анализируемого логического условия управление передается микрокоманде с адресом, который содержится в коде микрокоманды. В этом случае длина микрокоманды уменьшается, т.к. содержит код только одного адреса.

Автоматы, реализованные т.о., называют автоматами с программируемой (гибкой) логикой в отличие от автоматов, схемы которых строятся на основе дискретных элементов – автоматов с жесткой логикой.

В первом случае структура УА включает в себя ЗУ и схему выбора адреса следующей команды (иногда еще схему формирования выходных сигналов микроопераций); во втором – схему их дискретных компонентов, состоящую из элементов памяти и комбинационных элементов.

Оба способа реализации получили дальнейшее развитие на основе программируемых БИС, МП и однородных сред.

ЛИТЕРАТУРА

1. Глушков В.М. Синтез цифровых автоматов. М.: 1967

2. Самофалов К.Г. и др. Прикладная теория цифровых автоматов. К.: 1987

3. Самофалов К.Г., Корнейчук В.И., Тарасенко В.П. Цифровые электронные вычислительные машины. - К.: Выща шк., 1983

4. Савельев А.Я. Прикладная теория цифровых автоматов. М.: 1987

5. Справочник по интегральным микросхемам /Под ред. Б.В. Тарабрина. - М.: Энергия, 1980.

6. Каган Б.М., Сташин В.В. Основы проектирования микропроцессорных устройств автоматики. М.: 1987

7. Руденко В.С., Сенько В.И., Чиженко И.М. Основы преобразовательной техники: Учебник для вузов. – 2-е изд., перераб. и доп. – М.: Высш. школа, 1980. – 424с.

8. Шило В.Л. Популярные цифровые микросхемы: Справочник. – М.: Радио и связь, 1988. – 352с.

9. Пухальский Г.И., Новосельцева Т.Я. Проектирование дискретных устройств на интегральных микросхемах: Справочник. – М.: Радио и связь, 1990. – 304с.

10. Зубчук В.И., Сигорский В.П., Шкуро А.Н. Справочник по цифровой схемотехнике. – К.: Тэхника, 1990. – 448с.

Дата добавления: 2014-01-06